Useful Code Snippets and FAQ¶
Code examples below that use sfepy-* scripts assume the sfepy package to be installed, see also Installation.
1. Installation¶
1.1 No module named 'sfepy.discrete.common.extmods.mappings'¶
When installing SfePy from sources or using the git version, its extension modules have to be compiled before using the package, see Compilation of C Extension Modules.
1.2 ModuleNotFoundError: No module named 'sfepy' + in-place compilation¶
The extension modules are compiled in place, but ModuleNotFoundError: No
module named 'sfepy' shows up when running some interactive
examples/scripts/modules from the SfePy source directory.
On some platforms the current directory is not in the sys.path directory
list. Add it using:
export PYTHONPATH=.
or add the following code prior to sfepy imports into the module:
import sys
sys.path.append('.')
3. Regions¶
3.1 Verify that regions are correctly defined¶
Using the problem description files (declarative API):
sfepy-run sfepy/examples/diffusion/poisson_short_syntax.py --save-regions-as-groups --solve-not sfepy-view -e cylinder_regions.vtk
In a script (imperative API):
problem.save_regions_as_groups('regions')
3.2 Define a region using a function of coordinates with the imperative API¶
Examples:
A facet region defined using a function of mesh vertex coordinates:
from sfepy.discrete import Function, Functions def _get_region(coors, domain=None): ii = np.nonzero(coors[:,0] < 0.5)[0] return ii get_region = Function('get_region', _get_region) region = domain.create_region( 'Region', 'vertices by get_region', 'facet', functions=Functions([get_region]), )
Analogously a cell region defined using the coordinates of cell centroids:
# ... region = domain.create_region( 'Region', 'cells by get_region', 'cell', functions=Functions([get_region]), )
4. Material parameters¶
4.1 How to set material parameters per region with the imperative API?¶
Example: define rho, D to have different values in regions omega1,
omega2:
m = Material('m', values={'rho': {'omega1': 2700, 'omega2': 6000},
'D': {'omega1': D1, 'omega2': D2}})
4.2 How to implement state dependent materials?¶
Besides writing a custom solver, one can use pseudo-time-stepping for this purpose, as demonstrated in linear_elasticity/material_nonlinearity.py or diffusion/poisson_field_dependent_material.py. Note that the examples are contrived, and in practice care must be taken to ensure convergence.
4.3 2D and 3D linear elasticity consistency¶
Why are results of a 2D elasticity simulation not consistent with a properly constrained 3D elasticity simulation?
Possible reason: when using the Young’s modulus and Poisson’s ratio as input
parameters, and then calling stiffness_from_youngpoisson(), note that the default
value of the plane argument is 'strain', corresponding to the plane
strain assumption, see also lame_from_youngpoisson(). Try setting
plane='stress'.
4.4 How to set material parameters by a function with the imperative API?¶
Example (also showing the full material function signature):
from sfepy.discrete import Material, Function
def get_pars(ts, coors, mode=None,
equations=None, term=None, problem=None, **kwargs):
value1 = a_function(ts.t, coors)
value2 = another_function(ts.step, coors)
if mode == 'qp':
out = {
'value1' : value1.reshape(coors.shape[0], 1, 1),
'value2' : value2.reshape(coors.shape[0], 1, 1),
}
return out
m = Material('m', function=Function('get_pars', get_pars))
4.5 How to get cells corresponding to coordinates in a material function?¶
The full signature of the material function is:
def get_pars(ts, coors, mode=None,
equations=None, term=None, problem=None, **kwargs)
Thus it has access to term.region.cells, hence access to the cells that
correspond to the coordinates. The length of the coors is n_cell *
n_qp, where n_qp is the number of quadrature points per cell, and
n_cell = len(term.region.cells), so that coors.reshape((n_cell, n_qp,
-1)) can be used.
4.6 Ordering of symmetric tensor components - no Voigt notation!¶
Due to historical reasons, SfePy does not use the Voigt notation for storing 3D symmetric
tensors. Instead, the ordering found in Crisfield [1] is used, where e.g. the
stress tensor components stored in a vector are ordered as ![[11, 22, 33,
12, 13, 23]](_images/math/c9b16ea0f2338a14e35327dda57164b08229a665.png) . That is, the
. That is, the 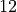 and
and 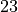 components are swapped
w.r.t. the Voigt notation. The same holds for the strain vector or the
components are swapped
w.r.t. the Voigt notation. The same holds for the strain vector or the
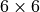 stiffness matrix.
stiffness matrix.
5. Solvers¶
5.1 How to work with solvers/preconditioners?¶
See multi_physics/biot_short_syntax.py (user-defined preconditioners) or navier_stokes/stokes_slip_bc.py (petsc solver setup).
5.2 How to get the linear system components: the matrix and the right-hand side?¶
To get the residual vector r (see Implementation of Essential Boundary Conditions) and the
tangent matrix K, the imperative API can be used as follows:
# pb is a Problem instance,
pb.set_bcs(ebcs=Conditions([...])) # Set Dirichlet boundary conditions.
pb.set_ics(Conditions([...])) # Set initial conditions (if any).
variables = pb.get_initial_state()
pb.time_update()
pb.update_materials()
variables.apply_ebc()
r = pb.equations.eval_residuals(variables())
K = pb.equations.eval_tangent_matrices(variables(), pb.mtx_a)
6. Postprocessing and visualization¶
6.1 Higher order DOF visualization for an approximation order greater than one¶
By default, the additional, higher order DOFs, are not used in the VTK/HDF5
results files ('strip' linearization kind). To see the influence of those
DOFs, 'adaptive' linearization has to be used, see diffusion/sinbc.py
(declarative API) and diffusion/laplace_refine_interactive.py or
multi_physics/biot_parallel_interactive.py (imperative API, search
linearization).
7. Finite element method implementation¶
7.1 Finite element approximation (field) order and numerical quadrature order¶
SfePy supports reading only straight-facet (linear approximation) meshes, nevertheless field orders higher than one can be used, because internally, the mesh elements are enriched with the required additional nodes. The calculation then occurs on such an augmented mesh with appropriate higher order elements.
The quadrature order equal to two-times the field order (used in many examples)
works well for bilinear forms with constant (on each element) material
parameters. For example, a dot product involves integrating u * v, so if
the approximation order of u and v is 1, their product’s order is 2. Of
course, there are terms that could use a lower quadrature order, or higher,
depending on the data. Increased quadrature order is required e.g. in terms
with highly oscillating material coefficients.
Example:
approx_order = 2
# The finite element approximation order.
fields = {
'displacement': ('real', 3, 'Omega', approx_order),
}
# The numerical quadrature order.
integrals = {
'i' : 2 * approx_order,
}
7.2 Numbering of DOFs¶
Locally (in a connectivity row), the DOFs are stored DOF-by-DOF (u_0 in all
local nodes, u_1 in all local nodes, …).
Globally (in a state vector), the DOFs are stored node-by-node
(u_0, u_1, ..., u_X in node 0, u_0, u_1, ..., u_X in node 1, …).
See also create_adof_conn().
7.3 Where is the code that calculates the element (e.g. stiffness) matrix?¶
The code that computes the per element residuals and matrices is organized in terms, see Term Overview - click on the term class name and then “source” link to see the code. The original terms are implemented in C, newer terms tend to be implemented directly in Python. The structure and attributes of a term class are described in How to Implement a New Term.
7.4 What structural elements are available in SfePy?¶
The code is currently focused on solid elements. The only supported structural elements are
shell10x, see linear_elasticity/shell10x_cantilever.py,
Mooney-Rivlin membrane with plain stress assumption, see large_deformation/balloon.py,
linear truss, see linear_elasticity/truss_bridge.py, linear_elasticity/truss_bridge3d.py,
linear spring elements, see linear_elasticity/multi_point_constraints.py.