sfepy.homogenization.utils module

sfepy.homogenization.utils.build_op_pi(var, ir, ic)[source]

Pi_i^{rs} = y_s delta_{ir} for r = ir, s = ic.

sfepy.homogenization.utils.coor_to_sym(ir, ic, dim)[source]
sfepy.homogenization.utils.create_pis(problem, var_name)[source]

Pi_i^{rs} = y_s delta_{ir}, ul{y} in Y coordinates.

sfepy.homogenization.utils.create_scalar_pis(problem, var_name)[source]

Pi^k = y_k, ul{y} in Y coordinates.

sfepy.homogenization.utils.define_box_regions(dim, lbn, rtf=None, eps=0.001, kind='facet')[source]

Define sides and corner regions for a box aligned with coordinate axes.

Parameters:
dimint

Space dimension

lbntuple

Left bottom near point coordinates if rtf is not None. If rtf is None, lbn are the (positive) distances from the origin.

rtftuple

Right top far point coordinates.

epsfloat

A parameter, that should be smaller than the smallest mesh node distance.

kindbool, optional

The region kind.

Returns:
regionsdict

The box regions.

sfepy.homogenization.utils.get_box_volume(dim, lbn, rtf=None)[source]

Volume of a box aligned with coordinate axes.

Parameters:

dimint

Space dimension

lbntuple

Left bottom near point coordinates if rtf is not None. If rtf is None, lbn are the (positive) distances from the origin.

rtftuple

Right top far point coordinates.

Returns:

volumefloat

The box volume.

sfepy.homogenization.utils.get_lattice_volume(axes)[source]

Volume of a periodic cell in a rectangular 3D (or 2D) lattice.

Parameters:
axesarray

The array with the periodic cell axes 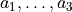a_1, \dots, a_3 as rows.

Returns:
volumefloat

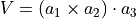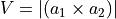The periodic cell volume V = (a_1 \times a_2) \cdot a_3. In 2D V = |(a_1 \times a_2)| with zeros as the third components of vectors a_1, a_2.

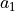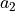sfepy.homogenization.utils.get_volume(problem, field_name, region_name, quad_order=1)[source]

Get volume of a given region using integration defined by a given field. Both the region and the field have to be defined in problem.

sfepy.homogenization.utils.integrate_in_time(coef, ts, scheme='forward')[source]

Forward difference or trapezoidal rule. ‘ts’ can be anything with ‘times’ attribute.

sfepy.homogenization.utils.interp_conv_mat(mat, ts, tdiff)[source]
sfepy.homogenization.utils.iter_nonsym(dim)[source]
sfepy.homogenization.utils.iter_sym(dim)[source]
sfepy.homogenization.utils.rm_multi(s)[source]
sfepy.homogenization.utils.set_nonlin_states(variables, nl_state, problem)[source]

Setup reference state for nonlinear homogenization

Parameters:
variablesdict

All problem variables

nl_statereference state
problemproblem description