linear_elasticity/its2D_4.py

Description

Diametrically point loaded 2-D disk with postprocessing and probes. See Primer.

1. solve the problem:

   sfepy-run sfepy/examples/linear_elasticity/its2D_4.py

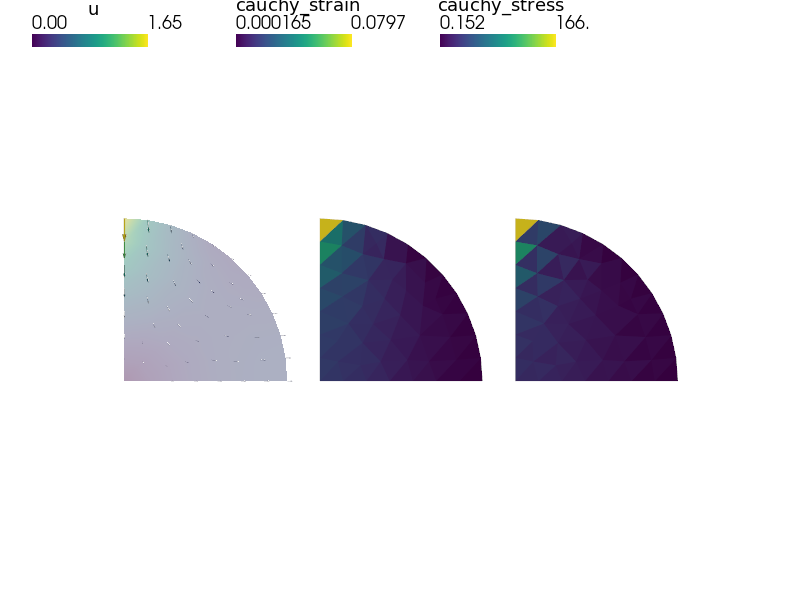
2. optionally, view the results:

   sfepy-view its2D.h5 -2

3. optionally, convert results to VTK, and view again ((assumes running from the sfepy directory):

   python3 sfepy/scripts/extractor.py -d its2D.h5 sfepy-view its2D.0.vtk -2

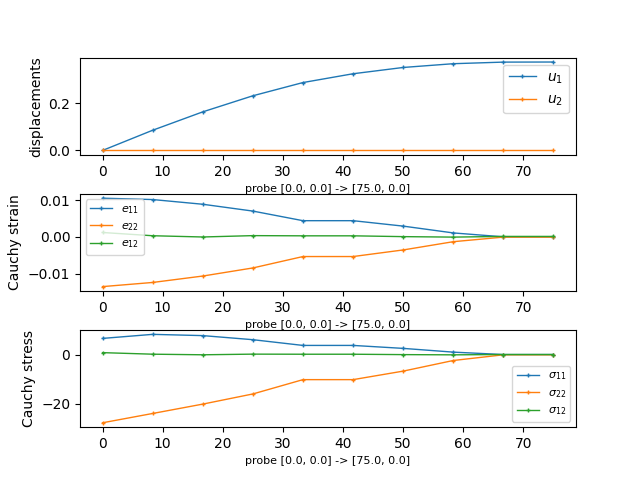
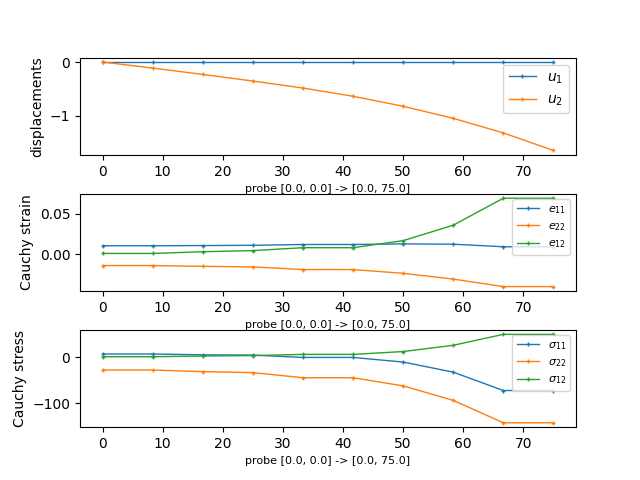
4. probe the data:

   sfepy-probe sfepy/examples/linear_elasticity/its2D_4.py its2D.h5

Find 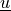such that:

where

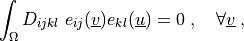
source code

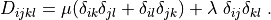
r"""
Diametrically point loaded 2-D disk with postprocessing and probes. See
:ref:`sec-primer`.

1. solve the problem::

   sfepy-run sfepy/examples/linear_elasticity/its2D_4.py

2. optionally, view the results::

   sfepy-view its2D.h5 -2

3. optionally, convert results to VTK, and view again ((assumes running from
   the sfepy directory)::

   python3 sfepy/scripts/extractor.py -d its2D.h5
   sfepy-view its2D.0.vtk -2

4. probe the data::

   sfepy-probe sfepy/examples/linear_elasticity/its2D_4.py its2D.h5

Find :math:`\ul{u}` such that:

.. math::
    \int_{\Omega} D_{ijkl}\ e_{ij}(\ul{v}) e_{kl}(\ul{u})
    = 0
    \;, \quad \forall \ul{v} \;,

where

.. math::
    D_{ijkl} = \mu (\delta_{ik} \delta_{jl}+\delta_{il} \delta_{jk}) +
    \lambda \ \delta_{ij} \delta_{kl}
    \;.
"""
from __future__ import absolute_import
from sfepy.examples.linear_elasticity.its2D_1 import *

from sfepy.mechanics.matcoefs import stiffness_from_youngpoisson
from six.moves import range

def stress_strain(out, pb, state, extend=False):
    """
    Calculate and output strain and stress for given displacements.
    """
    from sfepy.base.base import Struct

    ev = pb.evaluate
    strain = ev('ev_cauchy_strain.2.Omega(u)', mode='el_avg')
    stress = ev('ev_cauchy_stress.2.Omega(Asphalt.D, u)', mode='el_avg')

    out['cauchy_strain'] = Struct(name='output_data', mode='cell',
                                  data=strain, dofs=None)
    out['cauchy_stress'] = Struct(name='output_data', mode='cell',
                                  data=stress, dofs=None)

    return out

def gen_lines(problem):
    from sfepy.discrete.probes import LineProbe
    ps0 = [[0.0,  0.0], [ 0.0,  0.0]]
    ps1 = [[75.0, 0.0], [ 0.0, 75.0]]

    # Use adaptive probe with 10 inital points.
    n_point = -10

    labels = ['%s -> %s' % (p0, p1) for p0, p1 in zip(ps0, ps1)]
    probes = []
    for ip in range(len(ps0)):
        p0, p1 = ps0[ip], ps1[ip]
        probes.append(LineProbe(p0, p1, n_point))

    return probes, labels


def probe_hook(data, probe, label, problem):
    import matplotlib.pyplot as plt
    import matplotlib.font_manager as fm

    def get_it(name, var_name):
        var = problem.create_variables([var_name])[var_name]
        var.set_data(data[name].data)

        pars, vals = probe(var)
        vals = vals.squeeze()
        return pars, vals

    results = {}
    results['u'] = get_it('u', 'u')
    results['cauchy_strain'] = get_it('cauchy_strain', 's')
    results['cauchy_stress'] = get_it('cauchy_stress', 's')

    fig = plt.figure()
    plt.clf()
    fig.subplots_adjust(hspace=0.4)
    plt.subplot(311)
    pars, vals = results['u']
    for ic in range(vals.shape[1]):
        plt.plot(pars, vals[:,ic], label=r'$u_{%d}$' % (ic + 1),
                 lw=1, ls='-', marker='+', ms=3)
    plt.ylabel('displacements')
    plt.xlabel('probe %s' % label, fontsize=8)
    plt.legend(loc='best', prop=fm.FontProperties(size=10))

    sym_indices = ['11', '22', '12']

    plt.subplot(312)
    pars, vals = results['cauchy_strain']
    for ic in range(vals.shape[1]):
        plt.plot(pars, vals[:,ic], label=r'$e_{%s}$' % sym_indices[ic],
                 lw=1, ls='-', marker='+', ms=3)
    plt.ylabel('Cauchy strain')
    plt.xlabel('probe %s' % label, fontsize=8)
    plt.legend(loc='best', prop=fm.FontProperties(size=8))

    plt.subplot(313)
    pars, vals = results['cauchy_stress']
    for ic in range(vals.shape[1]):
        plt.plot(pars, vals[:,ic], label=r'$\sigma_{%s}$' % sym_indices[ic],
                 lw=1, ls='-', marker='+', ms=3)
    plt.ylabel('Cauchy stress')
    plt.xlabel('probe %s' % label, fontsize=8)
    plt.legend(loc='best', prop=fm.FontProperties(size=8))

    return plt.gcf(), results

materials['Asphalt'][0].update({'D' : stiffness_from_youngpoisson(2, young, poisson)})

# Update fields and variables to be able to use probes for tensors.
fields.update({
    'sym_tensor': ('real', 3, 'Omega', 0),
})

variables.update({
    's' : ('parameter field', 'sym_tensor', None),
})

options.update({
    'output_format'     : 'h5', # VTK reader cannot read cell data yet for probing
    'post_process_hook' : 'stress_strain',
    'gen_probes'        : 'gen_lines',
    'probe_hook'        : 'probe_hook',
})