acoustics/vibro_acoustic3d.py¶
Description
Vibro-acoustic problem
3D acoustic domain with 2D perforated deforming interface.
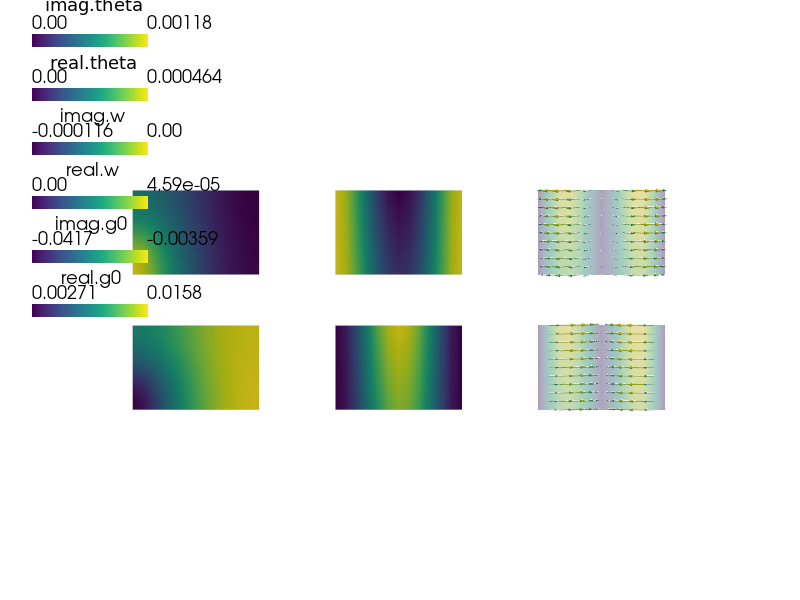
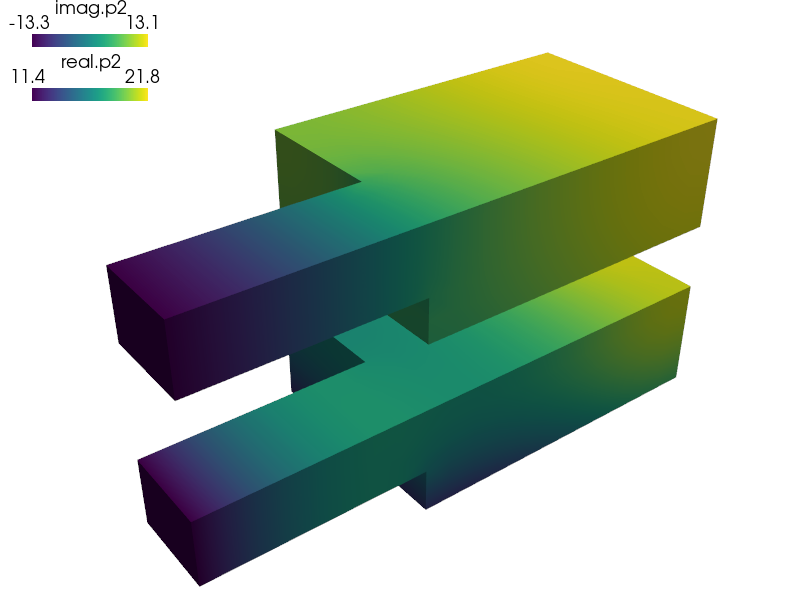
Problem definition - find 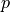 (acoustic pressure),
(acoustic pressure),
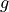 (transversal acoustic velocity),
(transversal acoustic velocity),
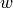 (plate deflection) and
(plate deflection) and 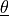 (rotation) such that:
(rotation) such that:
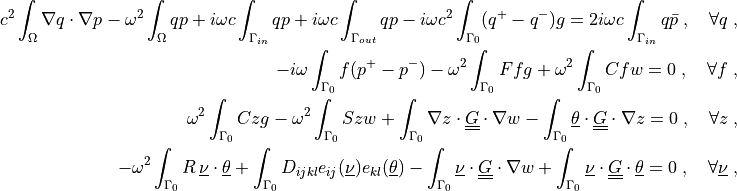

r"""
Vibro-acoustic problem
3D acoustic domain with 2D perforated deforming interface.
Problem definition - find :math:`p` (acoustic pressure),
:math:`g` (transversal acoustic velocity),
:math:`w` (plate deflection) and :math:`\ul{\theta}` (rotation) such that:
.. math::
c^2 \int_{\Omega} \nabla q \cdot \nabla p
- \omega^2 \int_{\Omega} q p
+ i \omega c \int_{\Gamma_{in}} q p
+ i \omega c \int_{\Gamma_{out}} q p
- i \omega c^2 \int_{\Gamma_0} (q^+ - q^-) g
= 2i \omega c \int_{\Gamma_{in}} q \bar{p}
\;, \quad \forall q \;,
- i \omega \int_{\Gamma_0} f (p^+ - p^-)
- \omega^2 \int_{\Gamma_0} F f g
+ \omega^2 \int_{\Gamma_0} C f w
= 0
\;, \quad \forall f \;,
\omega^2 \int_{\Gamma_0} C z g
- \omega^2 \int_{\Gamma_0} S z w
+ \int_{\Gamma_0} \nabla z \cdot \ull{G} \cdot \nabla w
- \int_{\Gamma_0} \ul{\theta} \cdot \ull{G} \cdot \nabla z
= 0
\;, \quad \forall z \;,
- \omega^2 \int_{\Gamma_0} R\, \ul{\nu} \cdot \ul{\theta}
+ \int_{\Gamma_0} D_{ijkl} e_{ij}(\ul{\nu}) e_{kl}(\ul{\theta})
- \int_{\Gamma_0} \ul{\nu} \cdot \ull{G} \cdot \nabla w
+ \int_{\Gamma_0} \ul{\nu} \cdot \ull{G} \cdot \ul{\theta}
= 0
\;, \quad \forall \ul{\nu} \;,
"""
import numpy as nm
from sfepy import data_dir
from sfepy.mechanics.matcoefs import stiffness_from_lame
def define(sound_speed=343.0,
wave_num=5.5,
p_inc=300,
thickness=0.01,
filename_mesh='/meshes/3d/acoustic_wg.vtk'):
filename_mesh = data_dir + filename_mesh
c = sound_speed
c2 = c**2
w = wave_num * c
w2 = w**2
wc = w * c
wc2 = w * c2
regions = {
'Omega1': 'cells of group 1',
'Omega2': 'cells of group 2',
'GammaIn': ('vertices of group 1', 'face'),
'GammaOut': ('vertices of group 2', 'face'),
'Gamma_aux': ('r.Omega1 *v r.Omega2', 'face'),
'Gamma0_1': ('copy r.Gamma_aux', 'face', 'Omega1'),
'Gamma0_2': ('copy r.Gamma_aux', 'face', 'Omega2'),
'Gamma0': ('copy r.Gamma_aux', 'cell', None, {'mesh_dim': 2}),
'Left_': ('vertices in (x < 0.001)', 'edge'),
'Right_': ('vertices in (x > 0.299)', 'edge'),
'Gamma0_Left': ('r.Gamma_aux *v r.Left_', 'edge'),
'Gamma0_Right': ('r.Gamma_aux *v r.Right_', 'edge'),
}
fields = {
'pressure1': ('complex', 'scalar', 'Omega1', 1),
'pressure2': ('complex', 'scalar', 'Omega2', 1),
'tvelocity': ('complex', 'scalar', 'Gamma0', 1),
'deflection': ('complex', 'scalar', 'Gamma0', 1),
'rotation': ('complex', 'vector', 'Gamma0', 1),
}
variables = {
'p1': ('unknown field', 'pressure1', 0),
'q1': ('test field', 'pressure1', 'p1'),
'p2': ('unknown field', 'pressure2', 1),
'q2': ('test field', 'pressure2', 'p2'),
'g0': ('unknown field', 'tvelocity', 2),
'f0': ('test field', 'tvelocity', 'g0'),
'w': ('unknown field', 'deflection', 3),
'z': ('test field', 'deflection', 'w'),
'theta': ('unknown field', 'rotation', 4),
'nu': ('test field', 'rotation', 'theta'),
}
ebcs = {
'fixed_l': ('Gamma0_Left', {'w.0': 0.0, 'theta.all': 0.0}),
'fixed_r': ('Gamma0_Right', {'w.0': 0.0, 'theta.all': 0.0}),
}
options = {
'split_results_by': 'region',
'output_dir': 'output',
}
functions = {
}
materials = {
'ac': ({
'F': -2.064e+00,
'c': -1.064e+00,
'T': 9.202e-01,
'hG': thickness * 4.5e10 * nm.eye(2),
'hR': thickness * 0.71,
'h3R': thickness**3 / 3.0 * 0.71,
'h3C': thickness**3 / 3.0 * stiffness_from_lame(2, 1e1, 1e0)}, ),
}
equations = {
'eq_p1': """
%e * dw_laplace.5.Omega1(q1, p1)
- %e * dw_dot.5.Omega1(q1, p1)
+ %s * dw_dot.5.GammaIn(q1, p1)
- %s * dw_dot.5.Gamma0_1(q1, tr(Gamma0, g0))
= %s * dw_integrate.5.GammaIn(q1)""" % (c2, w2, 1j * wc,
1j * wc2, 2j * wc * p_inc),
'eq_p2': """
+ %e * dw_laplace.5.Omega2(q2, p2)
- %e * dw_dot.5.Omega2(q2, p2)
+ %s * dw_dot.5.GammaOut(q2, p2)
+ %s * dw_dot.5.Gamma0_2(q2, tr(Gamma0, g0))
= 0""" % (c2, w2, 1j * wc, 1j * wc2),
'eq_g0': """
- %s * dw_dot.5.Gamma0(f0, tr(Gamma0_1, p1))
+ %s * dw_dot.5.Gamma0(f0, tr(Gamma0_2, p2))
- %e * dw_dot.5.Gamma0(ac.F, f0, g0)
+ %e * dw_dot.5.Gamma0(ac.c, f0, w)
= 0""" % (1j * w, 1j * w, w2, w2),
'eq_w': """
%e * dw_dot.5.Gamma0(ac.c, z, g0)
- %e * dw_dot.5.Gamma0(ac.T, z, w)
- %e * dw_dot.5.Gamma0(ac.hR, z, w)
+ dw_diffusion.5.Gamma0(ac.hG, z, w)
- dw_v_dot_grad_s.5.Gamma0(ac.hG, theta, z)
= 0""" % (w2, w2, w2),
'eq_theta': """
- %e * dw_dot.5.Gamma0(ac.h3R, nu, theta)
+ dw_lin_elastic.5.Gamma0(ac.h3C, nu, theta)
- dw_v_dot_grad_s.5.Gamma0(ac.hG, nu, w)
+ dw_dot.5.Gamma0(ac.hG, nu, theta)
= 0""" % (w2, ),
}
solvers = {
'ls': ('ls.auto_direct', {}),
'nls': ('nls.newton', {
'i_max': 1,
'eps_a': 1e-4,
'eps_r': 1e-6,
})
}
return locals()