sfepy.terms.terms_mass module¶

class sfepy.terms.terms_mass.MassTerm(*args, **kwargs)[source]¶

Mass term with lumping and RMM support [1].

The lumping parameter can be ‘row_sum’, ‘hrz’ or ‘none’ (default). It applies for $\beta$ > 0:

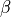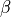$\beta$ = 0 correponds to the consistent mass matrix $M^C$ ;
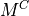0 < 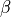$\beta$ < 1 corresponds to the averaged mass matrix $M^A$ .
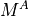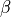$\beta$ = 1 corresponds to the lumped mass matrix $M^L$ ;

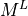term_mode can be None (default), ‘DPM’ (diagonal projection matrix 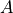$A$ ), or ‘RMM’ (reciprocal mass matrix $C$ ).

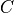[1]

González, J.A., Kolman, R., Cho, S.S., Felippa, C.A., Park, K.C., 2018. Inverse mass matrix via the method of localized Lagrange multipliers. International Journal for Numerical Methods in Engineering 113, 277–295. https://doi.org/10.1002/nme.5613

Definition:

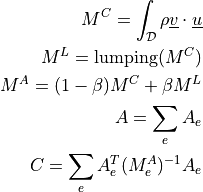
$M^C = \int_{\cal{D}} \rho \ul{v} \cdot \ul{u} \\ M^L = \mathrm{lumping}(M^C) \\ M^A = (1 - \beta) M^C + \beta M^L \\ A = \sum_e A_e \\ C = \sum_e A_e^T (M_e^A)^{-1} A_e$

Call signature:

de_mass

(material_rho, material_lumping, material_beta, virtual, state)

Arguments:

material: $\rho$
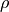
material: lumping
material: $\beta$
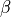
virtual/parameter_1: $\ul{v}$
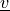
state/parameter_2: $\ul{u}$

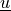
arg_shapes = {'material_beta': '.: 1', 'material_lumping': '.: str', 'material_rho': '1, 1', 'state': 'D', 'virtual': ('D', 'state')}¶

arg_types = ('material_rho', 'material_lumping', 'material_beta', 'virtual', 'state')¶

get_function(rho, lumping, beta, virtual, state, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

modes = ('weak', 'eval')¶

name = 'de_mass'¶