sfepy.terms.terms_flexo module¶
Flexoelectricity related terms.
- class sfepy.terms.terms_flexo.MixedFlexoCouplingTerm(*args, **kwargs)[source]¶
Flexoelectric coupling term, mixed formulation.
- Definition:
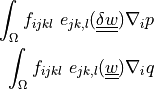
- Call signature:
de_m_flexo_coupling
(material, virtual, state)(material, state, virtual)(material, parameter_t, parameter_s)- Arguments 1:
material:
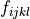
virtual/parameter_t:
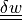
state/parameter_s:

- Arguments 2:
material:
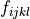
state :
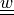
virtual :

- arg_shapes = [{'material': 'D, SD', 'parameter_s': 1, 'parameter_t': 'D2', 'state/dp-w': 'D2', 'state/dw-p': 1, 'virtual/dp-w': (1, None), 'virtual/dw-p': ('D2', None)}]¶
- arg_types = (('material', 'virtual', 'state'), ('material', 'state', 'virtual'), ('material', 'parameter_t', 'parameter_s'))¶
- modes = ('dw-p', 'dp-w', 'eval')¶
- name = 'de_m_flexo_coupling'¶
- class sfepy.terms.terms_flexo.MixedFlexoTerm(*args, **kwargs)[source]¶
Mixed formulation displacement gradient consistency term.
- Definition:
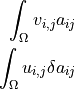
- Call signature:
de_m_flexo
(virtual, state)(state, virtual)(parameter_v, parameter_t)- Arguments 1:
virtual/parameter_v:
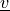
state/parameter_t:
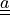
- Arguments 2:
state :
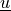
virtual :
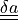
- arg_shapes = [{'parameter_t': 'D2', 'parameter_v': 'D', 'state/da-u': 'D', 'state/du-a': 'D2', 'virtual/da-u': ('D2', None), 'virtual/du-a': ('D', None)}, {'opt_material': None}]¶
- arg_types = (('virtual', 'state'), ('state', 'virtual'), ('parameter_v', 'parameter_t'))¶
- modes = ('du-a', 'da-u', 'eval')¶
- name = 'de_m_flexo'¶
- class sfepy.terms.terms_flexo.MixedStrainGradElasticTerm(*args, **kwargs)[source]¶
Flexoelectric strain gradient elasticity term, mixed formulation.
Additional evaluation modes:
‘strain’ - compute strain from the displacement gradient (state) variable.
- Definition:
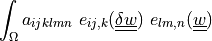
- Call signature:
de_m_sg_elastic
(material, virtual, state)(material, parameter_1, parameter_2)- Arguments:
material:
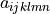
virtual/parameter_1:
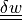
state/parameter_2:
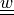
- arg_shapes = {'material': 'SD, SD', 'parameter_1': 'D2', 'parameter_2': 'D2', 'state': 'D2', 'virtual': ('D2', 'state')}¶
- arg_types = (('material', 'virtual', 'state'), ('material', 'parameter_1', 'parameter_2'))¶
- modes = ('weak', 'eval')¶
- name = 'de_m_sg_elastic'¶