sfepy.terms.terms_fibres module¶
- class sfepy.terms.terms_fibres.FibresActiveTLTerm(*args, **kwargs)[source]¶
Hyperelastic active fibres term. Effective stress
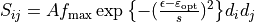 ,
where
,
where 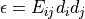 is the Green strain
is the Green strain
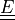 projected to the fibre direction
projected to the fibre direction 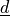 .
.- Definition:
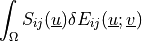
- Call signature:
dw_tl_fib_a
(material_1, material_2, material_3, material_4, material_5, virtual, state)- Arguments:
material_1 :
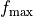
material_2 :
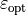
material_3 :

material_4 :
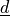
material_5 :
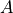
virtual :
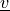
state :
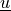
- arg_shapes = {'material_1': '1, 1', 'material_2': '1, 1', 'material_3': '1, 1', 'material_4': 'D, 1', 'material_5': '1, 1', 'state': 'D', 'virtual': ('D', 'state')}¶
- arg_types = ('material_1', 'material_2', 'material_3', 'material_4', 'material_5', 'virtual', 'state')¶
- family_data_names = ['green_strain']¶
- get_eval_shape(mat1, mat2, mat3, mat4, mat5, virtual, state, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶
- get_fargs(mat1, mat2, mat3, mat4, mat5, virtual, state, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶
- name = 'dw_tl_fib_a'¶
- class sfepy.terms.terms_fibres.FibresExponentialTLTerm(*args, **kwargs)[source]¶
Hyperelastic fibres term with an exponential response. Effective stress
![S_{ij} = \max\left(0, \sigma \left[ \exp{\left\{k (\epsilon -
\epsilon_0)\right\}} - 1 \right]\right) d_i d_j](../../../_images/math/818be169bffbc9bb528ab15a4dde4f62851b4fc8.png) , where
, where 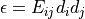 is the Green strain
is the Green strain 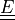 projected to the fibre
direction
projected to the fibre
direction 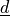 .
.- Definition:
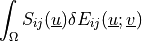
- Call signature:
dw_tl_fib_e
(material_1, material_2, material_3, material_4, virtual, state)- Arguments:
material_1 :
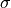
material_3 :
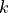
material_3 :
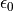
material_4 :
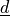
virtual :
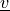
state :
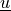
- arg_shapes = {'material_1': '1, 1', 'material_2': '1, 1', 'material_3': '1, 1', 'material_4': 'D, 1', 'state': 'D', 'virtual': ('D', 'state')}¶
- arg_types = ('material_1', 'material_2', 'material_3', 'material_4', 'virtual', 'state')¶
- family_data_names = ['green_strain']¶
- get_eval_shape(mat1, mat2, mat3, mat4, virtual, state, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶
- get_fargs(mat1, mat2, mat3, mat4, virtual, state, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶
- name = 'dw_tl_fib_e'¶
- class sfepy.terms.terms_fibres.FibresSoftPlusExponentialTLTerm(*args, **kwargs)[source]¶
Hyperelastic fibres term with an exponential response. Effective stress
![S_{ij} = \max\left(0, \sigma \left[ e^{k (\epsilon - \epsilon_0)} -
1 \right]\right) d_i d_j](../../../_images/math/a5770a11ee0eaddf4acc5de91832947a46d81b0a.png) , where
, where 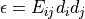 is the
Green strain
is the
Green strain 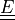 projected to the fibre direction
projected to the fibre direction
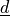 . The
. The 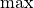 is approximated by the softplus function
scaled by
is approximated by the softplus function
scaled by 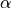 , i.e.
, i.e. 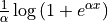 .
.- Definition:
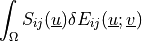
- Call signature:
dw_tl_fib_spe
(opt_material_0, material_1, material_2, material_3, material_4, virtual, state)- Arguments:
material_0 :
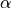 (default: 50)
(default: 50)material_1 :
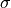
material_3 :
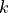
material_3 :
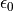
material_4 :
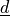
virtual :
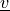
state :
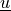
- arg_shapes = [{'material_1': '1, 1', 'material_2': '1, 1', 'material_3': '1, 1', 'material_4': 'D, 1', 'opt_material_0': '.: 1', 'state': 'D', 'virtual': ('D', 'state')}, {'opt_material_0': None}]¶
- arg_types = ('opt_material_0', 'material_1', 'material_2', 'material_3', 'material_4', 'virtual', 'state')¶
- family_data_names = ['green_strain']¶
- get_eval_shape(mat1, mat2, mat3, mat4, mat5, virtual, state, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶
- get_fargs(mat0, mat1, mat2, mat3, mat4, virtual, state, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶
- name = 'dw_tl_fib_spe'¶
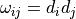 .
.