sfepy.terms.terms_dot module¶
- class sfepy.terms.terms_dot.BCNewtonTerm(name, arg_str, integral, region, **kwargs)[source]¶
Newton boundary condition term.
- Definition:
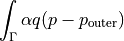
- Call signature:
dw_bc_newton
(material_1, material_2, virtual, state)- Arguments:
material_1 :
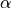
material_2 :

virtual :

state :

- arg_shapes = {'material_1': '1, 1', 'material_2': '1, 1', 'state': 1, 'virtual': (1, 'state')}¶
- arg_shapes_dict = None¶
- arg_types = ('material_1', 'material_2', 'virtual', 'state')¶
- get_fargs(alpha, p_outer, virtual, state, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶
- integration = 'facet'¶
- mode = 'weak'¶
- name = 'dw_bc_newton'¶
- class sfepy.terms.terms_dot.DotProductTerm(name, arg_str, integral, region, **kwargs)[source]¶
Volume and surface
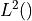 weighted dot product for both
scalar and vector fields. If the region is a surface and
either virtual or state variable is a vector, the orientation
of the normal vectors is outwards to the parent region of the virtual
variable. Can be evaluated. Can use derivatives.
weighted dot product for both
scalar and vector fields. If the region is a surface and
either virtual or state variable is a vector, the orientation
of the normal vectors is outwards to the parent region of the virtual
variable. Can be evaluated. Can use derivatives.- Definition:
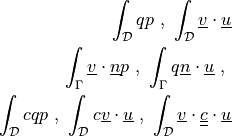
- Call signature:
dw_dot
(opt_material, virtual, state)(opt_material, parameter_1, parameter_2)- Arguments:
material:
 or
or 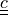 (optional)
(optional)virtual/parameter_1:
 or
or 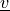
state/parameter_2:
 or
or 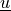
- arg_shapes_dict = {'cell': [{'opt_material': '1, 1', 'parameter_1': 1, 'parameter_2': 1, 'state': 1, 'virtual': (1, 'state')}, {'opt_material': None}, {'opt_material': '1, 1', 'parameter_1': 'D', 'parameter_2': 'D', 'state': 'D', 'virtual': ('D', 'state')}, {'opt_material': 'D, D'}, {'opt_material': None}], 'facet': [{'opt_material': '1, 1', 'parameter_1': 1, 'parameter_2': 1, 'state': 1, 'virtual': (1, 'state')}, {'opt_material': None}, {'opt_material': '1, 1', 'state': 'D', 'virtual': (1, None)}, {'opt_material': None}, {'opt_material': '1, 1', 'state': 1, 'virtual': ('D', None)}, {'opt_material': None}, {'opt_material': '1, 1', 'parameter_1': 'D', 'parameter_2': 'D', 'state': 'D', 'virtual': ('D', 'state')}, {'opt_material': 'D, D'}, {'opt_material': None}]}¶
- arg_types = (('opt_material', 'virtual', 'state'), ('opt_material', 'parameter_1', 'parameter_2'))¶
- integration = ('cell', 'facet')¶
- modes = ('weak', 'eval')¶
- name = 'dw_dot'¶
- class sfepy.terms.terms_dot.DotSProductVolumeOperatorWETHTerm(name, arg_str, integral, region, **kwargs)[source]¶
Fading memory volume
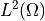 weighted dot product for
scalar fields. This term has the same definition as
dw_volume_dot_w_scalar_th, but assumes an exponential approximation of
the convolution kernel resulting in much higher efficiency. Can use
derivatives.
weighted dot product for
scalar fields. This term has the same definition as
dw_volume_dot_w_scalar_th, but assumes an exponential approximation of
the convolution kernel resulting in much higher efficiency. Can use
derivatives.- Definition:
![\int_\Omega \left [\int_0^t \Gcal(t-\tau) p(\tau) \difd{\tau} \right] q](../../../_images/math/2d499f8c27dae301afb76f8f374b19209c688ac1.png)
- Call signature:
dw_volume_dot_w_scalar_eth
(ts, material_0, material_1, virtual, state)- Arguments:
ts :
TimeStepperinstancematerial_0 :
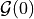
material_1 :
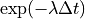 (decay at
(decay at 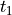 )
)virtual :

state :

- arg_shapes = {'material_0': '1, 1', 'material_1': '1, 1', 'state': 1, 'virtual': (1, 'state')}¶
- arg_types = ('ts', 'material_0', 'material_1', 'virtual', 'state')¶
- static function(out, coef, val_qp, rcmap, ccmap, is_diff)¶
- get_fargs(ts, mat0, mat1, virtual, state, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶
- name = 'dw_volume_dot_w_scalar_eth'¶
- class sfepy.terms.terms_dot.DotSProductVolumeOperatorWTHTerm(name, arg_str, integral, region, **kwargs)[source]¶
Fading memory volume
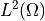 weighted dot product for
scalar fields. Can use derivatives.
weighted dot product for
scalar fields. Can use derivatives.- Definition:
![\int_\Omega \left [\int_0^t \Gcal(t-\tau) p(\tau) \difd{\tau} \right] q](../../../_images/math/2d499f8c27dae301afb76f8f374b19209c688ac1.png)
- Call signature:
dw_volume_dot_w_scalar_th
(ts, material, virtual, state)- Arguments:
ts :
TimeStepperinstancematerial :
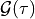
virtual :

state :

- arg_shapes = {'material': '.: N, 1, 1', 'state': 1, 'virtual': (1, 'state')}¶
- arg_types = ('ts', 'material', 'virtual', 'state')¶
- static function(out, coef, val_qp, rcmap, ccmap, is_diff)¶
- name = 'dw_volume_dot_w_scalar_th'¶
- class sfepy.terms.terms_dot.ScalarDotGradIScalarTerm(name, arg_str, integral, region, **kwargs)[source]¶
Dot product of a scalar and the
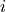 -th component of gradient of a
scalar. The index should be given as a ‘special_constant’ material
parameter.
-th component of gradient of a
scalar. The index should be given as a ‘special_constant’ material
parameter.- Definition:
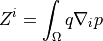
- Call signature:
dw_s_dot_grad_i_s
(material, virtual, state)- Arguments:
material :
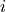
virtual :

state :

- arg_shapes = {'material': '.: 1, 1', 'state': 1, 'virtual': (1, 'state')}¶
- arg_types = ('material', 'virtual', 'state')¶
- name = 'dw_s_dot_grad_i_s'¶
- class sfepy.terms.terms_dot.ScalarDotMGradScalarTerm(name, arg_str, integral, region, **kwargs)[source]¶
Volume dot product of a scalar gradient dotted with a material vector with a scalar.
- Definition:
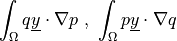
- Call signature:
dw_s_dot_mgrad_s
(material, virtual, state)(material, state, virtual)- Arguments 1:
material :
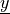
virtual :

state :

- Arguments 2:
material :
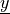
state :

virtual :

- arg_shapes = [{'material': 'D, 1', 'state/grad_state': 1, 'state/grad_virtual': 1, 'virtual/grad_state': (1, None), 'virtual/grad_virtual': (1, None)}]¶
- arg_types = (('material', 'virtual', 'state'), ('material', 'state', 'virtual'))¶
- modes = ('grad_state', 'grad_virtual')¶
- name = 'dw_s_dot_mgrad_s'¶
- class sfepy.terms.terms_dot.VectorDotGradScalarTerm(name, arg_str, integral, region, **kwargs)[source]¶
Volume dot product of a vector and a gradient of scalar. Can be evaluated.
- Definition:
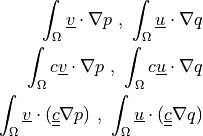
- Call signature:
dw_v_dot_grad_s
(opt_material, virtual, state)(opt_material, state, virtual)(opt_material, parameter_v, parameter_s)- Arguments 1:
material:
 or
or 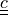 (optional)
(optional)virtual/parameter_v:
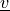
state/parameter_s:

- Arguments 2:
material :
 or
or 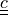 (optional)
(optional)state :
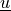
virtual :

- arg_shapes = [{'opt_material': '1, 1', 'parameter_s': 1, 'parameter_v': 'D', 'state/s_weak': 'D', 'state/v_weak': 1, 'virtual/s_weak': (1, None), 'virtual/v_weak': ('D', None)}, {'opt_material': 'D, D'}, {'opt_material': None}]¶
- arg_types = (('opt_material', 'virtual', 'state'), ('opt_material', 'state', 'virtual'), ('opt_material', 'parameter_v', 'parameter_s'))¶
- modes = ('v_weak', 's_weak', 'eval')¶
- name = 'dw_v_dot_grad_s'¶
- class sfepy.terms.terms_dot.VectorDotScalarTerm(name, arg_str, integral, region, **kwargs)[source]¶
Volume dot product of a vector and a scalar. Can be evaluated.
- Definition:
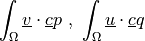
- Call signature:
dw_vm_dot_s
(material, virtual, state)(material, state, virtual)(material, parameter_v, parameter_s)- Arguments 1:
material :
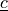
virtual/parameter_v:
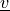
state/parameter_s:

- Arguments 2:
material :
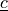
state :
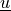
virtual :

- arg_shapes = [{'material': 'D, 1', 'parameter_s': 1, 'parameter_v': 'D', 'state/s_weak': 'D', 'state/v_weak': 1, 'virtual/s_weak': (1, None), 'virtual/v_weak': ('D', None)}]¶
- arg_types = (('material', 'virtual', 'state'), ('material', 'state', 'virtual'), ('material', 'parameter_v', 'parameter_s'))¶
- modes = ('v_weak', 's_weak', 'eval')¶
- name = 'dw_vm_dot_s'¶