sfepy.terms.terms_diffusion module¶
- class sfepy.terms.terms_diffusion.AdvectDivFreeTerm(name, arg_str, integral, region, **kwargs)[source]¶
Advection of a scalar quantity
 with the advection velocity
with the advection velocity
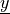 given as a material parameter (a known function of space and
time).
given as a material parameter (a known function of space and
time).The advection velocity has to be divergence-free!
- Definition:
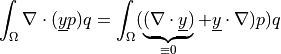
- Call signature:
dw_advect_div_free
(material, virtual, state)- Arguments:
material :
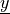
virtual :

state :

- arg_shapes = {'material': 'D, 1', 'state': '1', 'virtual': ('1', 'state')}¶
- arg_types = ('material', 'virtual', 'state')¶
- mode = 'grad_state'¶
- name = 'dw_advect_div_free'¶
- class sfepy.terms.terms_diffusion.ConvectVGradSTerm(name, arg_str, integral, region, **kwargs)[source]¶
Scalar gradient term with convective velocity.
- Definition:
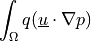
- Call signature:
dw_convect_v_grad_s
(virtual, state_v, state_s)- Arguments:
virtual :

state_v :
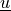
state_s :

- arg_shapes = [{'state_s': 1, 'state_v': 'D', 'virtual': (1, 'state_s')}]¶
- arg_types = ('virtual', 'state_v', 'state_s')¶
- static function(out, val_v, grad_s, cmap_v, cmap_s, is_diff)¶
- name = 'dw_convect_v_grad_s'¶
- class sfepy.terms.terms_diffusion.DiffusionCoupling(name, arg_str, integral, region, **kwargs)[source]¶
Diffusion copupling term with material parameter
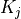 .
.- Definition:
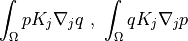
- Call signature:
dw_diffusion_coupling
(material, virtual, state)(material, state, virtual)(material, parameter_1, parameter_2)- Arguments:
material :
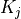
virtual :

state :

- arg_shapes = {'material': 'D, 1', 'parameter_1': 1, 'parameter_2': 1, 'state': 1, 'virtual': (1, 'state')}¶
- arg_types = (('material', 'virtual', 'state'), ('material', 'state', 'virtual'), ('material', 'parameter_1', 'parameter_2'))¶
- modes = ('weak0', 'weak1', 'eval')¶
- name = 'dw_diffusion_coupling'¶
- class sfepy.terms.terms_diffusion.DiffusionRTerm(name, arg_str, integral, region, **kwargs)[source]¶
Diffusion-like term with material parameter
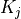 (to
use on the right-hand side).
(to
use on the right-hand side).- Definition:
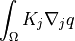
- Call signature:
dw_diffusion_r
(material, virtual)- Arguments:
material :
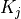
virtual :

- arg_shapes = {'material': 'D, 1', 'virtual': (1, None)}¶
- arg_types = ('material', 'virtual')¶
- static function(out, mtx_d, cmap)¶
- name = 'dw_diffusion_r'¶
- class sfepy.terms.terms_diffusion.DiffusionTerm(name, arg_str, integral, region, **kwargs)[source]¶
General diffusion term with permeability
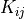 . Can be
evaluated. Can use derivatives.
. Can be
evaluated. Can use derivatives.- Definition:
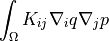
- Call signature:
dw_diffusion
(material, virtual, state)(material, parameter_1, parameter_2)- Arguments:
material:
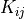
virtual/parameter_1:

state/parameter_2:

- arg_shapes = {'material': 'D, D', 'parameter_1': 1, 'parameter_2': 1, 'state': 1, 'virtual': (1, 'state')}¶
- arg_types = (('material', 'virtual', 'state'), ('material', 'parameter_1', 'parameter_2'))¶
- modes = ('weak', 'eval')¶
- name = 'dw_diffusion'¶
- symbolic = {'expression': 'div( K * grad( u ) )', 'map': {'K': 'material', 'u': 'state'}}¶
- class sfepy.terms.terms_diffusion.DiffusionVelocityTerm(name, arg_str, integral, region, **kwargs)[source]¶
Evaluate diffusion velocity.
Supports ‘eval’, ‘el_avg’ and ‘qp’ evaluation modes.
- Definition:
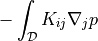
- Call signature:
ev_diffusion_velocity
(material, parameter)- Arguments:
material :
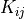
parameter :

- arg_shapes = {'material': 'D, D', 'parameter': 1}¶
- arg_types = ('material', 'parameter')¶
- integration = ('cell', 'facet_extra')¶
- name = 'ev_diffusion_velocity'¶
- class sfepy.terms.terms_diffusion.LaplaceTerm(name, arg_str, integral, region, **kwargs)[source]¶
Laplace term with
 coefficient. Can be
evaluated. Can use derivatives.
coefficient. Can be
evaluated. Can use derivatives.- Definition:
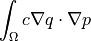
- Call signature:
dw_laplace
(opt_material, virtual, state)(opt_material, parameter_1, parameter_2)- Arguments 1:
material:

virtual/parameter_1:

state/parameter_2:

- arg_shapes = [{'opt_material': '1, 1', 'parameter_1': 1, 'parameter_2': 1, 'state': 1, 'virtual': (1, 'state')}, {'opt_material': None}]¶
- arg_types = (('opt_material', 'virtual', 'state'), ('opt_material', 'parameter_1', 'parameter_2'))¶
- modes = ('weak', 'eval')¶
- name = 'dw_laplace'¶
- symbolic = {'expression': 'c * div( grad( u ) )', 'map': {'c': 'opt_material', 'u': 'state'}}¶
- class sfepy.terms.terms_diffusion.NonlinearDiffusionTerm(name, arg_str, integral, region, **kwargs)[source]¶
The diffusion term with a scalar coefficient given by a user supplied function of the state variable.
- Definition:
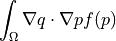
- Call signature:
dw_nl_diffusion
(fun, dfun, virtual, state)- Arguments:
fun :
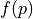
dfun :
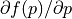
virtual :

state :

- arg_shapes = {'dfun': <function NonlinearDiffusionTerm.<lambda>>, 'fun': <function NonlinearDiffusionTerm.<lambda>>, 'state': 1, 'virtual': (1, 'state')}¶
- arg_types = ('fun', 'dfun', 'virtual', 'state')¶
- name = 'dw_nl_diffusion'¶
- class sfepy.terms.terms_diffusion.SDDiffusionTerm(name, arg_str, integral, region, **kwargs)[source]¶
Diffusion sensitivity analysis term.
- Definition:
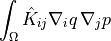
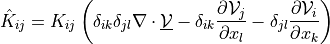
- Call signature:
ev_sd_diffusion
(material, parameter_q, parameter_p, parameter_mv)- Arguments:
material:
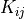
parameter_q:

parameter_p:

parameter_mv:
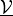
- arg_shapes = {'material': 'D, D', 'parameter_mv': 'D', 'parameter_p': 1, 'parameter_q': 1}¶
- arg_types = ('material', 'parameter_q', 'parameter_p', 'parameter_mv')¶
- static function(out, grad_q, grad_p, grad_w, div_w, mtx_d, cmap)¶
- get_eval_shape(mat, parameter_q, parameter_p, parameter_mv, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶
- get_fargs(mat, parameter_q, parameter_p, parameter_mv, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶
- name = 'ev_sd_diffusion'¶
- class sfepy.terms.terms_diffusion.SurfaceFluxOperatorTerm(name, arg_str, integral, region, **kwargs)[source]¶
Surface flux operator term.
- Definition:
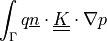
- Call signature:
dw_surface_flux
(opt_material, virtual, state)- Arguments:
material :
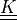
virtual :

state :

- arg_shapes = [{'opt_material': 'D, D', 'state': 1, 'virtual': (1, 'state')}, {'opt_material': None}]¶
- arg_types = ('opt_material', 'virtual', 'state')¶
- static function(out, grad, mat, bf, cmap, fis, mode)¶
- integration = 'facet_extra'¶
- name = 'dw_surface_flux'¶
- class sfepy.terms.terms_diffusion.SurfaceFluxTerm(name, arg_str, integral, region, **kwargs)[source]¶
Surface flux term.
Supports ‘eval’, ‘el_eval’ and ‘el_avg’ evaluation modes.
- Definition:
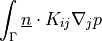
- Call signature:
ev_surface_flux
(material, parameter)- Arguments:
material:
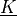
parameter:
 ,
,
- arg_shapes = {'material': 'D, D', 'parameter': 1}¶
- arg_types = ('material', 'parameter')¶
- static function(out, grad, mtx_d, cmap, mode)¶
- integration = 'facet_extra'¶
- name = 'ev_surface_flux'¶