sfepy.mechanics.membranes module¶
- sfepy.mechanics.membranes.create_mapping(coors, gel, order)[source]¶
Create mapping from transformed (in x-y plane) element faces to reference element faces.
- Parameters:
- coorsarray
The transformed coordinates of element nodes, shape (n_el, n_ep, dim). The function verifies that the all z components are zero.
- gelGeometryElement instance
The geometry element corresponding to the faces.
- orderint
The polynomial order of the mapping.
- Returns:
- mappingFEMapping instance
The reference element face mapping.
- sfepy.mechanics.membranes.create_transformation_matrix(coors)[source]¶
Create a transposed coordinate transformation matrix, that transforms 3D coordinates of element face nodes so that the transformed nodes are in the x-y plane. The rotation is performed w.r.t. the first node of each face.
- Parameters:
- coorsarray
The coordinates of element nodes, shape (n_el, n_ep, dim).
- Returns:
- mtx_tarray
The transposed transformation matrix
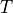 , i.e.
, i.e.
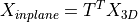 .
.
Notes
![T = [t_1, t_2, n]](../../../_images/math/4fff2b5da6da8807bad080ad935b16c2d65caf96.png) , where
, where 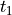 ,
, 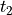 , are unit
in-plane (column) vectors and
, are unit
in-plane (column) vectors and 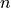 is the unit normal vector,
all mutually orthonormal.
is the unit normal vector,
all mutually orthonormal.
- sfepy.mechanics.membranes.describe_deformation(el_disps, bfg)[source]¶
Describe deformation of a thin incompressible 2D membrane in 3D space, composed of flat finite element faces.
The coordinate system of each element (face), i.e. the membrane mid-surface, should coincide with the x, y axes of the x-y plane.
- Parameters:
- el_dispsarray
The displacements of element nodes, shape (n_el, n_ep, dim).
- bfgarray
The in-plane base function gradients, shape (n_el, n_qp, dim-1, n_ep).
- Returns:
- mtx_c ; array
The in-plane right Cauchy-Green deformation tensor
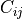 ,
, 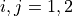 .
.- c33array
The component
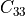 computed from the incompressibility
condition.
computed from the incompressibility
condition.- mtx_barray
The discrete Green strain variation operator.
- sfepy.mechanics.membranes.describe_geometry(field, region, integral)[source]¶
Describe membrane geometry in a given region.
- Parameters:
- fieldField instance
The field defining the FE approximation.
- regionRegion instance
The surface region to describe.
- integralIntegral instance
The integral defining the quadrature points.
- Returns:
- mtx_tarray
The transposed transformation matrix
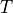 , see
, see
create_transformation_matrix().- membrane_geoCMapping instance
The mapping from transformed elements to a reference elements.
- sfepy.mechanics.membranes.get_green_strain_sym3d(mtx_c, c33)[source]¶
Get the 3D Green strain tensor in symmetric storage.
- Parameters:
- mtx_c ; array
The in-plane right Cauchy-Green deformation tensor
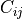 ,
, 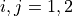 , shape (n_el, n_qp, dim-1,
dim-1).
, shape (n_el, n_qp, dim-1,
dim-1).- c33array
The component
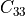 computed from the incompressibility
condition, shape (n_el, n_qp).
computed from the incompressibility
condition, shape (n_el, n_qp).
- Returns:
- mtx_earray
The membrane Green strain
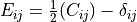 , symmetric storage: items (11, 22, 33, 12, 13, 23),
shape (n_el, n_qp, sym, 1).
, symmetric storage: items (11, 22, 33, 12, 13, 23),
shape (n_el, n_qp, sym, 1).
- sfepy.mechanics.membranes.get_invariants(mtx_c, c33)[source]¶
Get the first and second invariants of the right Cauchy-Green deformation tensor describing deformation of an incompressible membrane.
- Parameters:
- mtx_c ; array
The in-plane right Cauchy-Green deformation tensor
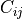 ,
, 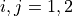 , shape (n_el, n_qp, dim-1,
dim-1).
, shape (n_el, n_qp, dim-1,
dim-1).- c33array
The component
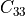 computed from the incompressibility
condition, shape (n_el, n_qp).
computed from the incompressibility
condition, shape (n_el, n_qp).
- Returns:
- i1array
The first invariant of
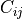 .
.- i2array
The second invariant of
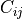 .
.
- sfepy.mechanics.membranes.get_tangent_stress_matrix(stress, bfg)[source]¶
Get the tangent stress matrix of a thin incompressible 2D membrane in 3D space, given a stress.
- Parameters:
- stressarray
The components 11, 22, 12 of the second Piola-Kirchhoff stress tensor, shape (n_el, n_qp, 3, 1).
- bfgarray
The in-plane base function gradients, shape (n_el, n_qp, dim-1, n_ep).
- Returns:
- mtxarray
The tangent stress matrix, shape (n_el, n_qp, dim*n_ep, dim*n_ep).
- sfepy.mechanics.membranes.transform_asm_matrices(out, mtx_t)[source]¶
Transform matrix assembling contributions to global coordinate system, one node at a time.
- Parameters:
- outarray
The array of matrices, transformed in-place.
- mtx_tarray
The transposed transformation matrix
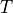 , see
, see
create_transformation_matrix().
- sfepy.mechanics.membranes.transform_asm_vectors(out, mtx_t)[source]¶
Transform vector assembling contributions to global coordinate system, one node at a time.
- Parameters:
- outarray
The array of vectors, transformed in-place.
- mtx_tarray
The transposed transformation matrix
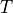 , see
, see
create_transformation_matrix().