sfepy.mechanics.matcoefs module¶
Conversion of material parameters and other utilities.
- class sfepy.mechanics.matcoefs.ElasticConstants(young=None, poisson=None, bulk=None, lam=None, mu=None, p_wave=None, _regenerate_relations=False)[source]¶
Conversion formulas for various groups of elastic constants. The elastic constants supported are:
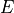 : Young’s modulus
: Young’s modulus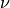 : Poisson’s ratio
: Poisson’s ratio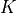 : bulk modulus
: bulk modulus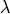 : Lamé’s first parameter
: Lamé’s first parameter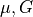 : shear modulus, Lamé’s second parameter
: shear modulus, Lamé’s second parameter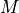 : P-wave modulus, longitudinal wave modulus
: P-wave modulus, longitudinal wave modulus
The elastic constants are referred to by the following keyword arguments: young, poisson, bulk, lam, mu, p_wave.
Exactly two of them must be provided to the __init__() method.
Examples
basic usage:
>>> from sfepy.mechanics.matcoefs import ElasticConstants >>> ec = ElasticConstants(lam=1.0, mu=1.5) >>> ec.young 3.6000000000000001 >>> ec.poisson 0.20000000000000001 >>> ec.bulk 2.0 >>> ec.p_wave 4.0 >>> ec.get(['bulk', 'lam', 'mu', 'young', 'poisson', 'p_wave']) [2.0, 1.0, 1.5, 3.6000000000000001, 0.20000000000000001, 4.0]
reinitialize existing instance:
>>> ec.init(p_wave=4.0, bulk=2.0) >>> ec.get(['bulk', 'lam', 'mu', 'young', 'poisson', 'p_wave']) [2.0, 1.0, 1.5, 3.6000000000000001, 0.20000000000000001, 4.0]
- class sfepy.mechanics.matcoefs.TransformToPlane(iplane=None)[source]¶
Transformations of constitutive law coefficients of 3D problems to 2D.
- tensor_plane_stress(c3=None, d3=None, b3=None)[source]¶
Transforms all coefficients of the piezoelectric constitutive law from 3D to plane stress problem in 2D: strain/stress ordering: 11 22 33 12 13 23. If d3 is None, uses only the stiffness tensor c3.
- Parameters:
- c3array
The stiffness tensor.
- d3array
The dielectric tensor.
- b3array
The piezoelectric coupling tensor.
- sfepy.mechanics.matcoefs.bulk_from_lame(lam, mu)[source]¶
Compute bulk modulus from Lamé parameters.
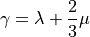
- sfepy.mechanics.matcoefs.bulk_from_youngpoisson(young, poisson, plane='strain')[source]¶
Compute bulk modulus corresponding to Young’s modulus and Poisson’s ratio.
- sfepy.mechanics.matcoefs.lame_from_stiffness(stiffness, plane='strain')[source]¶
Compute Lamé parameters from an isotropic stiffness tensor.
- sfepy.mechanics.matcoefs.lame_from_youngpoisson(young, poisson, plane='strain')[source]¶
Compute Lamé parameters from Young’s modulus and Poisson’s ratio.
The relationship between Lamé parameters and Young’s modulus, Poisson’s ratio (see [1],[2]):
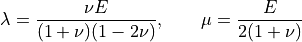
The plain stress hypothesis:
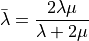
[1] I.S. Sokolnikoff: Mathematical Theory of Elasticity. New York, 1956.
[2] T.J.R. Hughes: The Finite Element Method, Linear Static and Dynamic Finite Element Analysis. New Jersey, 1987.
- sfepy.mechanics.matcoefs.stiffness_from_lame(dim, lam, mu)[source]¶
Compute stiffness tensor corresponding to Lamé parameters.
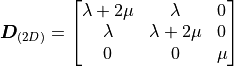
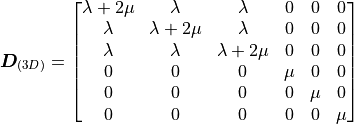
- sfepy.mechanics.matcoefs.stiffness_from_lame_mixed(dim, lam, mu)[source]¶
Compute stiffness tensor corresponding to Lamé parameters for mixed formulation.
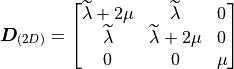
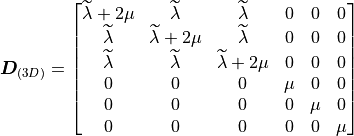
where
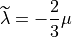
- sfepy.mechanics.matcoefs.stiffness_from_youngpoisson(dim, young, poisson, plane='strain')[source]¶
Compute stiffness tensor corresponding to Young’s modulus and Poisson’s ratio.
- sfepy.mechanics.matcoefs.stiffness_from_youngpoisson_mixed(dim, young, poisson, plane='strain')[source]¶
Compute stiffness tensor corresponding to Young’s modulus and Poisson’s ratio for mixed formulation.
- sfepy.mechanics.matcoefs.stiffness_from_yps_ortho3(young, poisson, shear)[source]¶
Compute 3D stiffness tensor
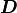 of an orthotropic linear
elastic material. Young’s modulus (
of an orthotropic linear
elastic material. Young’s modulus (![[E_1, E_2, E_3]](../../../_images/math/ffd935b1bc67d5324ed475a482995afea384452d.png) ),
Poisson’s ratio (
),
Poisson’s ratio (![[\nu_{12}, \nu_{13}, \nu_{23}]](../../../_images/math/89ee521c42c1ff1a365152299058fb54f1765b0b.png) ),
and shear modulus (
),
and shear modulus (![[G_{12}, G_{13}, G_{23}]](../../../_images/math/b07b59a6ccbe18ba45cc62fa3d0619c5c8aff8b8.png) ) are given.
) are given.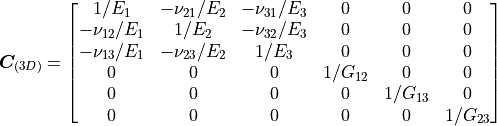
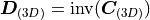
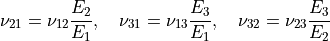
[1] R.M. Jones: Mechanics of composite materials. 1999.
- sfepy.mechanics.matcoefs.wave_speeds_from_youngpoisson(young, poisson, rho)[source]¶
Compute the P- and S-wave speeds from the Young’s modulus
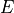 and
Poisson’s ratio
and
Poisson’s ratio 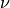 in a homogeneous isotropic material.
in a homogeneous isotropic material.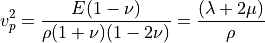
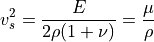
- Parameters:
- youngfloat or array
The Young’s modulus.
- poissonfloat or array
The Poisson’s ratio.
- rhofloat or array
The density.
- Returns:
- vpfloat or array
The P-wave speed.
- vsfloat or array
The S-wave speed.
- sfepy.mechanics.matcoefs.youngpoisson_from_stiffness(stiffness, plane='strain')[source]¶
Compute Young’s modulus and Poisson’s ratio from an isotropic stiffness tensor.
- sfepy.mechanics.matcoefs.youngpoisson_from_wave_speeds(vp, vs, rho)[source]¶
Compute the Young’s modulus
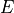 and Poisson’s ratio
and Poisson’s ratio 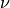 from
the P- and S-wave speeds in a homogeneous isotropic material.
from
the P- and S-wave speeds in a homogeneous isotropic material.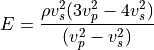
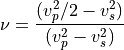
- Parameters:
- vpfloat or array
The P-wave speed.
- vsfloat or array
The S-wave speed.
- rhofloat or array
The density.
- Returns:
- youngfloat or array
The Young’s modulus.
- poissonfloat or array
The Poisson’s ratio.