sfepy.terms.terms_sensitivity module¶
- class sfepy.terms.terms_sensitivity.ESDDiffusionTerm(*args, **kwargs)[source]¶
Diffusion sensitivity analysis term.
- Definition:
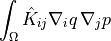
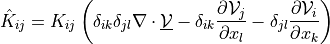
- Call signature:
de_sd_diffusion
(material, virtual, state, parameter_mv)(material, parameter_1, parameter_2, parameter_mv)- Arguments:
material:
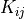
virtual/parameter_1:

state/parameter_2:

parameter_mv:
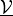
- arg_shapes = {'material': 'D, D', 'parameter_1': 1, 'parameter_2': 1, 'parameter_mv': 'D', 'state': 1, 'virtual': (1, 'state')}¶
- arg_types = (('material', 'virtual', 'state', 'parameter_mv'), ('material', 'parameter_1', 'parameter_2', 'parameter_mv'))¶
- modes = ('weak', 'eval')¶
- name = 'de_sd_diffusion'¶
- class sfepy.terms.terms_sensitivity.ESDDivGradTerm(*args, **kwargs)[source]¶
Sensitivity (shape derivative) of diffusion term de_div_grad.
- Definition:
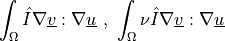
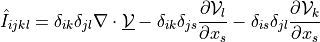
- Call signature:
de_sd_div_grad
(opt_material, virtual, state, parameter_mv)(opt_material, parameter_1, parameter_2, parameter_mv)- Arguments:
material:
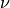 (viscosity, optional)
(viscosity, optional)virtual/parameter_1:
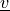
state/parameter_2:
parameter_mv:
- arg_shapes = [{'opt_material': '1, 1', 'parameter_1': 'D', 'parameter_2': 'D', 'parameter_mv': 'D', 'state': 'D', 'virtual': ('D', 'state')}, {'opt_material': None}]¶
- arg_types = (('opt_material', 'virtual', 'state', 'parameter_mv'), ('opt_material', 'parameter_1', 'parameter_2', 'parameter_mv'))¶
- modes = ('weak', 'eval')¶
- name = 'de_sd_div_grad'¶
- class sfepy.terms.terms_sensitivity.ESDDotTerm(*args, **kwargs)[source]¶
Sensitivity (shape derivative) of dot product of scalars or vectors.
- Definition:
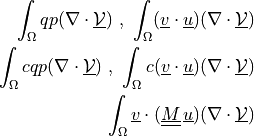
- Call signature:
de_sd_dot
(opt_material, virtual, state, parameter_mv)(opt_material, parameter_1, parameter_2, parameter_mv)- Arguments:
material:
 or
or 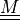 (optional)
(optional)virtual/parameter_1:
 or
or 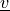
state/parameter_2:
 or
or 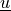
parameter_mv :
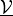
- arg_shapes = [{'opt_material': '1, 1', 'parameter_1': 1, 'parameter_2': 1, 'parameter_mv': 'D', 'state': 1, 'virtual': (1, 'state')}, {'opt_material': None}, {'opt_material': '1, 1', 'parameter_1': 'D', 'parameter_2': 'D', 'parameter_mv': 'D', 'state': 'D', 'virtual': ('D', 'state')}, {'opt_material': 'D, D'}, {'opt_material': None}]¶
- arg_types = (('opt_material', 'virtual', 'state', 'parameter_mv'), ('opt_material', 'parameter_1', 'parameter_2', 'parameter_mv'))¶
- modes = ('weak', 'eval')¶
- name = 'de_sd_dot'¶
- class sfepy.terms.terms_sensitivity.ESDLinearElasticTerm(*args, **kwargs)[source]¶
Sensitivity analysis of the linear elastic term.
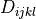 can be given in symmetric or non-symmetric form.
can be given in symmetric or non-symmetric form.- Definition:
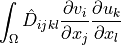
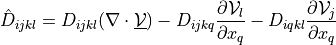
- Call signature:
de_sd_lin_elastic
(material, virtual, state, parameter_mv)(material, parameter_1, parameter_2, parameter_mv)- Arguments 1:
material :
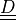
virtual/parameter_v :
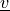
state/parameter_s :
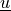
parameter_mv :
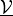
- arg_shapes = [{'material': 'S, S', 'parameter_1': 'D', 'parameter_2': 'D', 'parameter_mv': 'D', 'state': 'D', 'virtual': ('D', 'state')}, {'material': 'D2, D2'}]¶
- arg_types = (('material', 'virtual', 'state', 'parameter_mv'), ('material', 'parameter_1', 'parameter_2', 'parameter_mv'))¶
- geometries = ['2_3', '2_4', '3_4', '3_8']¶
- modes = ('weak', 'eval')¶
- name = 'de_sd_lin_elastic'¶
- class sfepy.terms.terms_sensitivity.ESDLinearTractionTerm(*args, **kwargs)[source]¶
Sensitivity of the linear traction term.
- Definition:
![\int_{\Gamma} \ul{v} \cdot \left[\left(\ull{\hat{\sigma}}\,
\nabla \cdot \ul{\cal{V}} - \ull{{\hat\sigma}}\, \nabla \ul{\cal{V}}
\right)\ul{n}\right]](../../../_images/math/8bddc4644c8bc14a19e70cb68c7d575b7ddb4c80.png)
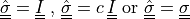
- Call signature:
de_sd_surface_ltr
(opt_material, virtual, parameter_mv)(opt_material, parameter, parameter_mv)- Arguments:
material:
 ,
, 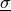 ,
, 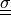
virtual/parameter:
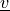
parameter_mv:
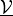
- arg_shapes = [{'opt_material': 'S, 1', 'parameter': 'D', 'parameter_mv': 'D', 'virtual': ('D', None)}, {'opt_material': None}, {'opt_material': '1, 1'}, {'opt_material': 'D, D'}]¶
- arg_types = (('opt_material', 'virtual', 'parameter_mv'), ('opt_material', 'parameter', 'parameter_mv'))¶
- integration = 'facet'¶
- modes = ('weak', 'eval')¶
- name = 'de_sd_surface_ltr'¶
- class sfepy.terms.terms_sensitivity.ESDPiezoCouplingTerm(*args, **kwargs)[source]¶
Sensitivity (shape derivative) of the piezoelectric coupling term.
- Definition:
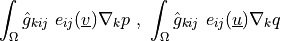
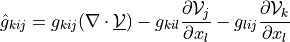
- Call signature:
de_sd_piezo_coupling
(material, virtual, state, parameter_mv)(material, state, virtual, parameter_mv)(material, parameter_v, parameter_s, parameter_mv)- Arguments 1:
material :
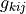
virtual/parameter_v :
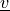
state/parameter_s :

parameter_mv :
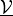
- Arguments 2:
material :
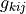
state :
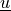
virtual :

parameter_mv :
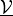
- arg_shapes = {'material': 'D, S', 'parameter_mv': 'D', 'parameter_s': 1, 'parameter_v': 'D', 'state/div': 'D', 'state/grad': 1, 'virtual/div': (1, None), 'virtual/grad': ('D', None)}¶
- arg_types = (('material', 'virtual', 'state', 'parameter_mv'), ('material', 'state', 'virtual', 'parameter_mv'), ('material', 'parameter_v', 'parameter_s', 'parameter_mv'))¶
- geometries = ['2_3', '2_4', '3_4', '3_8']¶
- modes = ('grad', 'div', 'eval')¶
- name = 'de_sd_piezo_coupling'¶
- class sfepy.terms.terms_sensitivity.ESDStokesTerm(*args, **kwargs)[source]¶
Stokes problem coupling term. Corresponds to weak forms of gradient and divergence terms.
- Definition:
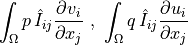
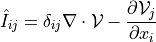
- Call signature:
de_sd_stokes
(opt_material, virtual, state, parameter_mv)(opt_material, state, virtual, parameter_mv)(opt_material, parameter_v, parameter_s, parameter_mv)- Arguments 1:
virtual/parameter_v:
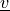
state/parameter_s:

parameter_mv:
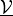
- Arguments 2:
state :
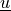
virtual :

parameter_mv:
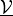
- arg_shapes = [{'opt_material': '1, 1', 'parameter_mv': 'D', 'parameter_s': 1, 'parameter_v': 'D', 'state/div': 'D', 'state/grad': 1, 'virtual/div': (1, None), 'virtual/grad': ('D', None)}, {'opt_material': None}]¶
- arg_types = (('opt_material', 'virtual', 'state', 'parameter_mv'), ('opt_material', 'state', 'virtual', 'parameter_mv'), ('opt_material', 'parameter_v', 'parameter_s', 'parameter_mv'))¶
- modes = ('grad', 'div', 'eval')¶
- name = 'de_sd_stokes'¶
- texpr = 'ij,i.j,0'¶
- class sfepy.terms.terms_sensitivity.ESDVectorDotGradScalarTerm(*args, **kwargs)[source]¶
Sensitivity of volume dot product of a vector and a gradient of scalar.
- Definition:
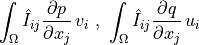
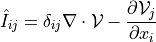
- Call signature:
de_sd_v_dot_grad_s
(opt_material, virtual, state, parameter_mv)(opt_material, state, virtual, parameter_mv)(opt_material, parameter_v, parameter_s, parameter_mv)- Arguments 1:
virtual/parameter_v:
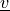
state/parameter_s:

parameter_mv:
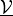
- Arguments 2:
state :
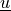
virtual :

parameter_mv:
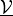
- name = 'de_sd_v_dot_grad_s'¶
- texpr = 'ij,i,0.j'¶