sfepy.terms.terms_piezo module¶
- class sfepy.terms.terms_piezo.PiezoCouplingTerm(name, arg_str, integral, region, **kwargs)[source]¶
Piezoelectric coupling term. Can be evaluated.
- Definition:
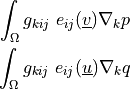
- Call signature:
dw_piezo_coupling
(material, virtual, state)(material, state, virtual)(material, parameter_v, parameter_s)- Arguments 1:
material:
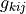
virtual/parameter_v:
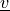
state/parameter_s:

- Arguments 2:
material :
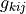
state :
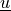
virtual :

- arg_shapes = {'material': 'D, S', 'parameter_s': 1, 'parameter_v': 'D', 'state/div': 'D', 'state/grad': 1, 'virtual/div': (1, None), 'virtual/grad': ('D', None)}¶
- arg_types = (('material', 'virtual', 'state'), ('material', 'state', 'virtual'), ('material', 'parameter_v', 'parameter_s'))¶
- modes = ('grad', 'div', 'eval')¶
- name = 'dw_piezo_coupling'¶
- class sfepy.terms.terms_piezo.PiezoStrainTerm(name, arg_str, integral, region, **kwargs)[source]¶
Evaluate piezoelectric strain tensor.
It is given in the usual vector form exploiting symmetry: in 3D it has 6 components with the indices ordered as
![[11, 22, 33, 12, 13, 23]](../../../_images/math/831e68247b7b81f4648d22336a8bd761038d0416.png) , in
2D it has 3 components with the indices ordered as
, in
2D it has 3 components with the indices ordered as ![[11, 22, 12]](../../../_images/math/f930f08c378137d074ca533e6d938267b04d560b.png) .
.Supports ‘eval’, ‘el_avg’ and ‘qp’ evaluation modes.
- Definition:
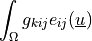
- Call signature:
ev_piezo_strain
(material, parameter)- Arguments:
material :
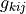
parameter :
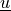
- arg_shapes = {'material': 'D, S', 'parameter': 'D'}¶
- name = 'ev_piezo_strain'¶
- class sfepy.terms.terms_piezo.PiezoStressTerm(name, arg_str, integral, region, **kwargs)[source]¶
Evaluate piezoelectric stress tensor.
It is given in the usual vector form exploiting symmetry: in 3D it has 6 components with the indices ordered as
![[11, 22, 33, 12, 13, 23]](../../../_images/math/831e68247b7b81f4648d22336a8bd761038d0416.png) , in
2D it has 3 components with the indices ordered as
, in
2D it has 3 components with the indices ordered as ![[11, 22, 12]](../../../_images/math/f930f08c378137d074ca533e6d938267b04d560b.png) .
.Supports ‘eval’, ‘el_avg’ and ‘qp’ evaluation modes.
- Definition:
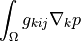
- Call signature:
ev_piezo_stress
(material, parameter)- Arguments:
material :
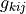
parameter :

- arg_shapes = {'material': 'D, S', 'parameter': '1'}¶
- arg_types = ('material', 'parameter')¶
- name = 'ev_piezo_stress'¶
- class sfepy.terms.terms_piezo.SDPiezoCouplingTerm(*args, **kwargs)[source]¶
Sensitivity (shape derivative) of the piezoelectric coupling term.
- Definition:
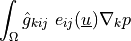
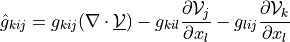
- Call signature:
ev_sd_piezo_coupling
(material, parameter_u, parameter_p, parameter_mv)- Arguments:
material :
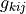
parameter_u :
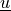
parameter_p :

parameter_mv :
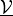
- arg_shapes = {'material': 'D, S', 'parameter_mv': 'D', 'parameter_p': 1, 'parameter_u': 'D'}¶
- arg_types = ('material', 'parameter_u', 'parameter_p', 'parameter_mv')¶
- geometries = ['2_3', '2_4', '3_4', '3_8']¶
- get_function(mat, par_u, par_p, par_mv, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶
- name = 'ev_sd_piezo_coupling'¶