sfepy.solvers.ts_dg_solvers module¶
Explicit time stepping solvers for use with DG FEM
- class sfepy.solvers.ts_dg_solvers.DGMultiStageTSS(conf, nls=None, context=None, **kwargs)[source]¶
Explicit time stepping solver with multistage solve_step method
Kind: ‘ts.multistaged’
For common configuration parameters, see
Solver.Specific configuration parameters:
- Parameters:
- t0float (default: 0.0)
The initial time.
- t1float (default: 1.0)
The final time.
- dtfloat
The time step. Used if n_step is not given.
- n_stepint (default: 10)
The number of time steps. Has precedence over dt.
- quasistaticbool (default: False)
If True, assume a quasistatic time-stepping. Then the non-linear solver is invoked also for the initial time.
- limitersdictionary
Limiters for DGFields, keys: field name, values: limiter class
- name = 'ts.multistaged'¶
- class sfepy.solvers.ts_dg_solvers.EulerStepSolver(conf, nls=None, context=None, **kwargs)[source]¶
Simple forward euler method
Kind: ‘ts.euler’
For common configuration parameters, see
Solver.Specific configuration parameters:
- Parameters:
- name = 'ts.euler'¶
- class sfepy.solvers.ts_dg_solvers.RK4StepSolver(conf, nls=None, context=None, **kwargs)[source]¶
Classical 4th order Runge-Kutta method, implemetantions is based on [1]
[1]Hesthaven, J. S., & Warburton, T. (2008). Nodal Discontinuous Galerkin Methods. Journal of Physics A: Mathematical and Theoretical (Vol. 54). New York, NY: Springer New York. http://doi.org/10.1007/978-0-387-72067-8, p. 63
Kind: ‘ts.runge_kutta_4’
For common configuration parameters, see
Solver.Specific configuration parameters:
- Parameters:
- name = 'ts.runge_kutta_4'¶
- stage_updates = (<function RK4StepSolver.<lambda>>, <function RK4StepSolver.<lambda>>, <function RK4StepSolver.<lambda>>, <function RK4StepSolver.<lambda>>)¶
- class sfepy.solvers.ts_dg_solvers.TVDRK3StepSolver(conf, nls=None, context=None, **kwargs)[source]¶
3rd order Total Variation Diminishing Runge-Kutta method based on [1]
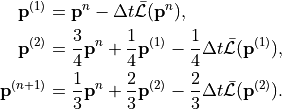 [1]
[1]Gottlieb, S., & Shu, C.-W. (2002). Total variation diminishing Runge-Kutta schemes. Mathematics of Computation of the American Mathematical Society, 67(221), 73–85. https://doi.org/10.1090/s0025-5718-98-00913-2
Kind: ‘ts.tvd_runge_kutta_3’
For common configuration parameters, see
Solver.Specific configuration parameters:
- Parameters:
- name = 'ts.tvd_runge_kutta_3'¶