sfepy.solvers.semismooth_newton module¶

class sfepy.solvers.semismooth_newton.SemismoothNewton(conf, **kwargs)[source]¶

The semi-smooth Newton method.

This method is suitable for solving problems of the following structure:

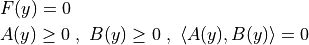
$\begin{split} & F(y) = 0 \\ & A(y) \ge 0 \;,\ B(y) \ge 0 \;,\ \langle A(y), B(y) \rangle = 0 \end{split}$

The function 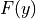$F(y)$ represents the smooth part of the problem.

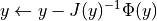
Regular step: $y \leftarrow y - J(y)^{-1} \Phi(y)$

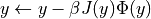
Steepest descent step: $y \leftarrow y - \beta J(y) \Phi(y)$

Although fun_smooth_grad() computes the gradient of the smooth part only, it should return the global matrix, where the non-smooth part is uninitialized, but pre-allocated.

Kind: ‘nls.semismooth_newton’

For common configuration parameters, see Solver.

Specific configuration parameters:

Parameters:

semismoothbool (default: True): If True, use the semi-smooth algorithm. Otherwise a non-smooth equation is assumed (use a brute force).
i_maxint (default: 1): The maximum number of iterations.
eps_afloat (default: 1e-10): The absolute tolerance for the residual, i.e. $||f(x^i)||$ .
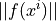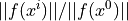eps_rfloat (default: 1.0): The relative tolerance for the residual, i.e. $||f(x^i)|| / ||f(x^0)||$ .
machepsfloat (default: 2.220446049250313e-16): The float considered to be machine “zero”.
lin_redfloat (default: 1.0): The linear system solution error should be smaller than (eps_a * lin_red), otherwise a warning is printed.
ls_onfloat (default: 0.99999): Start the backtracking line-search by reducing the step, if 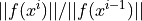$||f(x^i)|| / ||f(x^{i-1})||$ is larger than ls_on.
ls_reddict (default: {‘regular’: 0.1, ‘steepest_descent’: 0.01}): The step reduction factor in case of correct residual assembling for regular and steepest descent modes.
ls_red_warp0.0 < float < 1.0 (default: 0.001): The step reduction factor in case of failed residual assembling (e.g. the “warp violation” error caused by a negative volume element resulting from too large deformations).
ls_min0.0 < float < 1.0 (default: 1e-05): The minimum step reduction factor.

compute_jacobian(vec_x, fun_smooth_grad, fun_a_grad, fun_b_grad, vec_smooth_r, vec_a_r, vec_b_r)[source]¶

name = 'nls.semismooth_newton'¶