sfepy.discrete.fem.fields_base module

Notes

Important attributes of continuous (order > 0) Field and SurfaceField instances:

• vertex_remap : econn[:, :n_vertex] = vertex_remap[conn]

• vertex_remap_i : conn = vertex_remap_i[econn[:, :n_vertex]]

where conn is the mesh vertex connectivity, econn is the region-local field connectivity.

class sfepy.discrete.fem.fields_base.FEField(name, dtype, shape, region, approx_order=1)

Base class for finite element fields.

Notes

• interps and hence node_descs are per region (must have single geometry!)

Field shape information:

• shape - the shape of the basis functions in a point

• n_components - the number of DOFs per FE node

• val_shape - the shape of field value (the product of DOFs and basis functions) in a point

average_qp_to_vertices(data_qp, integral)

Average data given in quadrature points in region elements into region vertices.

clear_qp_basis()

Remove cached quadrature points and basis functions.

create_bqp(region_name, integral)

create_bqp_key(integral, bkey)

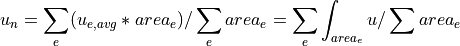
create_mapping(region, integral, integration, return_mapping=True)

Create a new reference mapping.

Compute jacobians, element volumes and basis function derivatives for Volume-type geometries (volume mappings), and jacobians, normals and basis function derivatives for Surface-type geometries (surface mappings).

Notes

• surface mappings are defined on the surface region

• surface mappings require field order to be > 0

create_mesh(extra_nodes=True)

Create a mesh from the field region, optionally including the field extra nodes.

create_output(dofs, var_name, dof_names=None, key=None, extend=True, fill_value=None, linearization=None)

Convert the DOFs corresponding to the field to a dictionary of output data usable by Mesh.write().

Parameters:

dofsarray, shape (n_nod, n_component)

The array of DOFs reshaped so that each column corresponds to one component.

var_namestr

The variable name corresponding to dofs.

dof_namestuple of str

The names of DOF components.

keystr, optional

The key to be used in the output dictionary instead of the variable name.

extendbool

Extend the DOF values to cover the whole domain.

fill_valuefloat or complex

The value used to fill the missing DOF values if extend is True.

linearizationStruct or None

The linearization configuration for higher order approximations.

Returns:

outdict

The output dictionary.

eval_basis(key, derivative, integral, iels=None, from_geometry=False, basis_only=True)

extend_dofs(dofs, fill_value=None)

Extend DOFs to the whole domain using the fill_value, or the smallest value in dofs if fill_value is None.

get_coor(nods=None)

Get coordinates of the field nodes.

Parameters:

nodsarray, optional

The indices of the required nodes. If not given, the coordinates of all the nodes are returned.

get_data_shape(integral, integration='cell', region_name=None)

Get element data dimensions.

Parameters:

integralIntegral instance

The integral describing used numerical quadrature.

integration‘cell’, ‘facet’, ‘facet_extra’, ‘point’ or ‘custom’

The term integration mode.

region_namestr

The name of the region of the integral.

Returns:

data_shape4 ints

The (n_el, n_qp, dim, n_en) for volume shape kind, (n_fa, n_qp, dim, n_fn) for surface shape kind and (n_nod, 0, 0, 1) for point shape kind.

Notes

Integration modes: - ‘cell’: integration over cells/elements - ‘facet’: integration over cell facets (faces, edges) - ‘facet_extra’: same as ‘facet’ but also the normal derivatives

are evaluated

• ‘point’: point integration

• ‘custom’: user defined integration

Dimensions: - n_el, n_fa = number of elements/facets - n_qp = number of quadrature points per element/facet - dim = spatial dimension - n_en, n_fn = number of element/facet nodes - n_nod = number of element nodes

get_dofs_in_region(region, merge=True)

Return indices of DOFs that belong to the given region.

get_econn(conn_type, region, trace_region=None, local=False)

Get extended connectivity of the given type in the given region.

Parameters:

conn_type: tuple or string

DOF connectivity type, eg. (‘cell’, 3) or ‘cell’. If the topological dimension not specified, it is taken from region.tdim.

region: sfepy.discrete.common.region.Region

The region for which the connectivity is required.

trace_region: None or string

If not None, return mirror connectivity according to local.

local: bool

If True, return local connectivity w.r.t. facet nodes, otherwise return global connectivity w.r.t. all mesh nodes.

Returns:

econn: numpy.ndarray

The extended connectivity array.

get_evaluate_cache(cache=None, share_geometry=False, verbose=False)

Get the evaluate cache for Variable.evaluate_at().

Parameters:

cacheStruct instance, optional

Optionally, use the provided instance to store the cache data.

share_geometrybool

Set to True to indicate that all the evaluations will work on the same region. Certain data are then computed only for the first probe and cached.

verbosebool

If False, reduce verbosity.

Returns:

cacheStruct instance

The evaluate cache.

get_output_approx_order()

Get the approximation order used in the output file.

get_qp(key, integral)

Get quadrature points and weights corresponding to the given key and integral. The key is ‘v’, ‘s#’ or ‘b#’, where # is the number of face vertices. For ‘b#’, the quadrature must already be created by calling FEField.create_bqp(), usually through FEField.create_mapping().

get_true_order()

Get the true approximation order depending on the reference element geometry.

For example, for P1 (linear) approximation the true order is 1, while for Q1 (bilinear) approximation in 2D the true order is 2.

get_vertices()

Return indices of vertices belonging to the field region.

interp_to_qp(dofs)

Interpolate DOFs into quadrature points.

The quadrature order is given by the field approximation order.

Parameters:

dofsarray

The array of DOF values of shape (n_nod, n_component).

Returns:

data_qparray

The values interpolated into the quadrature points.

integralIntegral

The corresponding integral defining the quadrature points.

is_higher_order()

Return True, if the field’s approximation order is greater than one.

linearize(dofs, min_level=0, max_level=1, eps=0.0001)

Linearize the solution for post-processing.

Parameters:

dofsarray, shape (n_nod, n_component)

The array of DOFs reshaped so that each column corresponds to one component.

min_levelint

The minimum required level of mesh refinement.

max_levelint

The maximum level of mesh refinement.

epsfloat

The relative tolerance parameter of mesh adaptivity.

Returns:

meshMesh instance

The adapted, nonconforming, mesh.

vdofsarray

The DOFs defined in vertices of mesh.

levelsarray of ints

The refinement level used for each element group.

remove_extra_dofs(dofs)

Remove DOFs defined in higher order nodes (order > 1).

restore_dofs(store=False)

Undoes the effect of FEField.substitute_dofs().

restore_substituted(vec)

Restore values of the unused DOFs using the transpose of the applied basis transformation.

set_basis_transform(transform)

Set local element basis transformation.

The basis transformation is applied in FEField.eval_basis() and FEField.create_mapping().

Parameters:

transformarray, shape (n_cell, n_ep, n_ep)

The array with (n_ep, n_ep) transformation matrices for each cell in the field’s region, where n_ep is the number of element DOFs.

set_coors(coors, extra_dofs=False)

Set coordinates of field nodes.

setup_bar_data(field, region)

setup_coors()

Setup coordinates of field nodes.

setup_extra_data(info)

setup_point_data(field, region)

setup_surface_data(region, trace_region=None)

nodes[leconn] == econn

substitute_dofs(subs, restore=False)

Perform facet DOF substitutions according to subs.

Modifies self.econn in-place and sets self.econn0, self.unused_dofs and self.basis_transform.

class sfepy.discrete.fem.fields_base.H1Mixin(**kwargs)

Methods of fields specific to H1 space.

sfepy.discrete.fem.fields_base.create_expression_output(expression, name, primary_field_name, fields, materials, variables, functions=None, mode='eval', term_mode=None, extra_args=None, verbose=True, kwargs=None, min_level=0, max_level=1, eps=0.0001)

Create output mesh and data for the expression using the adaptive linearizer.

Parameters:

expressionstr

The expression to evaluate.

namestr

The name of the data.

primary_field_namestr

The name of field that defines the element groups and polynomial spaces.

fieldsdict

The dictionary of fields used in variables.

materialsMaterials instance

The materials used in the expression.

variablesVariables instance

The variables used in the expression.

functionsFunctions instance, optional

The user functions for materials etc.

modeone of ‘eval’, ‘el_avg’, ‘qp’

The evaluation mode - ‘qp’ requests the values in quadrature points, ‘el_avg’ element averages and ‘eval’ means integration over each term region.

term_modestr

The term call mode - some terms support different call modes and depending on the call mode different values are returned.

extra_argsdict, optional

Extra arguments to be passed to terms in the expression.

verbosebool

If False, reduce verbosity.

kwargsdict, optional

The variables (dictionary of (variable name) : (Variable instance)) to be used in the expression.

min_levelint

The minimum required level of mesh refinement.

max_levelint

The maximum level of mesh refinement.

epsfloat

The relative tolerance parameter of mesh adaptivity.

Returns:

outdict

The output dictionary.

sfepy.discrete.fem.fields_base.eval_nodal_coors(coors, mesh_coors, region, poly_space, geom_poly_space, econn, only_extra=True)

Compute coordinates of nodes corresponding to poly_space, given mesh coordinates and geom_poly_space.

sfepy.discrete.fem.fields_base.get_eval_expression(expression, fields, materials, variables, functions=None, mode='eval', term_mode=None, extra_args=None, verbose=True, kwargs=None)

Get the function for evaluating an expression given a list of elements, and reference element coordinates.

sfepy.discrete.fem.fields_base.set_mesh_coors(domain, fields, coors, update_fields=False, actual=False, clear_all=True, extra_dofs=False)