sfepy.discrete.dg.poly_spaces module¶
- class sfepy.discrete.dg.poly_spaces.LegendrePolySpace(name, geometry, order, extended)[source]¶
Legendre hierarchical polynomials basis, over [0, 1] domain.
- get_interpol_scheme()[source]¶
For dim > 1 returns F and P matrices according to gmsh basis specification [1]: Let us assume that the approximation of the view’s value over an element is written as a linear combination of d basis functions
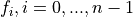 (the coefficients being stored
in list-of-values).
(the coefficients being stored
in list-of-values).Defining
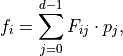
with
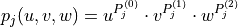 (u, v and w being the
coordinates in the element’s parameter space), then val-coef-matrix
denotes the n x n matrix F and val-exp-matrix denotes the n x 3 matrix P
where n is number of basis functions as calculated by
(u, v and w being the
coordinates in the element’s parameter space), then val-coef-matrix
denotes the n x n matrix F and val-exp-matrix denotes the n x 3 matrix P
where n is number of basis functions as calculated by get_n_el_nod.Expects matrices to be saved in atributes coefM and expoM!
[1]Remacle, J.-F., Chevaugeon, N., Marchandise, E., & Geuzaine, C. (2007). Efficient visualization of high-order finite elements. International Journal for Numerical Methods in Engineering, 69(4), 750-771. https://doi.org/10.1002/nme.1787
- Returns:
- interp_scheme_structStruct
Struct with name of the scheme, geometry desc and P and F
- get_nth_fun(n)[source]¶
Uses shifted Legendre polynomials formula on interval [0, 1].
Convenience function for testing
- Parameters:
- nint
- Returns:
- funcallable
n-th function of the legendre basis
- get_nth_fun_der(n, diff=1)[source]¶
Returns diff derivative of nth function. Uses shifted legendre polynomials formula on interval [0, 1].
Useful for testing.
- Parameters:
- nint
- diffint
(Default value = 1)
- Returns:
- funcallable
derivative of n-th function of the 1D legendre basis
- gradjacobiP(coors, alpha, beta, diff=1)[source]¶
diff derivative of the jacobi polynomials on interval [-1, 1] up to self.order + 1 at coors
- Parameters:
- coors
- alphafloat
- betafloat
- diffint
(Default value = 1)
- Returns:
- valuesndarray
output shape is shape(coor) + (self.order + 1,)
- gradlegendreP(coors, diff=1)[source]¶
- Parameters:
- diffint
default 1
- coorsarray_like
coordinates, preferably in interval [-1, 1] for which this basis is intented
- Returns:
- valuesndarray
values at coors of all the legendre polynomials up to self.order
- jacobiP(coors, alpha, beta)[source]¶
Values of the jacobi polynomials on interval [-1, 1] up to self.order + 1 at coors
- Parameters:
- coorsarray_like
- betafloat
- alphafloat
- Returns:
- valuesndarray
output shape is shape(coor) + (self.order + 1,)
- legendreP(coors)[source]¶
- Parameters:
- coorsarray_like
coordinates, preferably in interval [-1, 1] for which this basis is intented
- Returns:
- valuesndarray
values at coors of all the legendre polynomials up to self.order
- legendre_funs = [<function LegendrePolySpace.<lambda>>, <function LegendrePolySpace.<lambda>>, <function LegendrePolySpace.<lambda>>, <function LegendrePolySpace.<lambda>>, <function LegendrePolySpace.<lambda>>, <function LegendrePolySpace.<lambda>>]¶
- class sfepy.discrete.dg.poly_spaces.LegendreSimplexPolySpace(name, geometry, order, extended=False)[source]¶
- name = 'legendre_simplex'¶
- class sfepy.discrete.dg.poly_spaces.LegendreTensorProductPolySpace(name, geometry, order)[source]¶
- build_interpol_scheme()[source]¶
Builds F and P matrices returned by self.get_interpol_scheme.
Note that this function returns coeficients according to gmsh parametrization of Quadrangle i.e. [-1, 1] x [-1, 1] and hence the form of basis function is not the same as exhibited by the LegendreTensorProductPolySpace object which acts on parametrization [0, 1] x [0, 1].
- Returns:
- Fndarray
coefficient matrix
- Pndarray
exponent matrix
- name = 'legendre_tensor_product'¶
- sfepy.discrete.dg.poly_spaces.get_n_el_nod(order, dim, extended=False)[source]¶
Number of nodes per element for discontinuous legendre basis, i.e. number of iterations yielded by iter_by_order
When extended is False
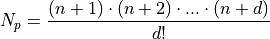
where n is the order and d the dimension. When extended is True
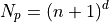
where n is the order and d the dimension.
- Parameters:
- orderint
desired order of multidimensional basis
- dimint
dimension of the basis
- extendedbool
iterate over extended tensor product basis (Default value = False)
- Returns:
- n_el_nodint
number of basis functions in basis
- sfepy.discrete.dg.poly_spaces.iter_by_order(order, dim, extended=False)[source]¶
Iterates over all combinations of basis functions indexes needed to create multidimensional basis in a way that creates hierarchical basis
- Parameters:
- orderint
desired order of multidimensional basis
- dimint
dimension of the basis
- extendedbool
iterate over extended tensor product basis (Default value = False)
- Yields:
- idxtuple
containing basis function indexes, used in
_combine_polyvalsand_combine_polyvals_der