large_deformation/compare_elastic_materials.py¶
Description
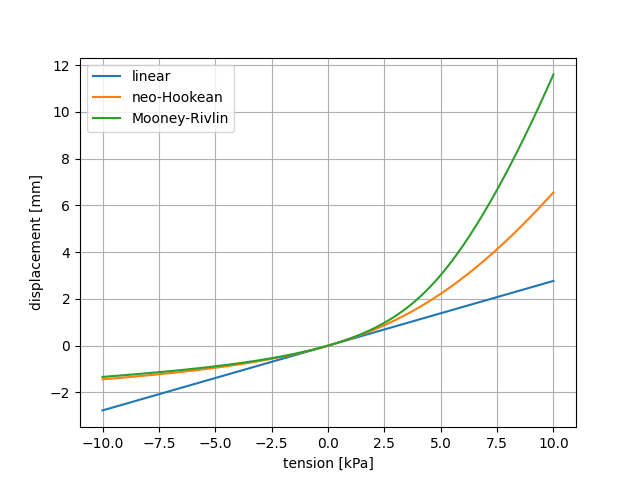
Compare various elastic materials w.r.t. uniaxial tension/compression test.
Requires Matplotlib.
#!/usr/bin/env python
"""
Compare various elastic materials w.r.t. uniaxial tension/compression test.
Requires Matplotlib.
"""
from __future__ import absolute_import
from argparse import ArgumentParser, RawDescriptionHelpFormatter
import sys
import six
sys.path.append('.')
import numpy as nm
def define():
"""Define the problem to solve."""
from sfepy.discrete.fem.meshio import UserMeshIO
from sfepy.mesh.mesh_generators import gen_block_mesh
from sfepy.mechanics.matcoefs import stiffness_from_lame
def mesh_hook(mesh, mode):
"""
Generate the block mesh.
"""
if mode == 'read':
mesh = gen_block_mesh([2, 2, 3], [2, 2, 4], [0, 0, 1.5], name='el3',
verbose=False)
return mesh
elif mode == 'write':
pass
filename_mesh = UserMeshIO(mesh_hook)
options = {
'nls' : 'newton',
'ls' : 'ls',
'ts' : 'ts',
'save_times' : 'all',
}
functions = {
'linear_tension' : (linear_tension,),
'linear_compression' : (linear_compression,),
'empty' : (lambda ts, coor, mode, region, ig: None,),
}
fields = {
'displacement' : ('real', 3, 'Omega', 1),
}
# Coefficients are chosen so that the tangent stiffness is the same for all
# material for zero strains.
# Young modulus = 10 kPa, Poisson's ratio = 0.3
materials = {
'solid' : ({
'K' : 8.333, # bulk modulus
'mu_nh' : 3.846, # shear modulus of neoHookean term
'mu_mr' : 1.923, # shear modulus of Mooney-Rivlin term
'kappa' : 1.923, # second modulus of Mooney-Rivlin term
# elasticity for LE term
'D' : stiffness_from_lame(dim=3, lam=5.769, mu=3.846),
},),
'load' : 'empty',
}
variables = {
'u' : ('unknown field', 'displacement', 0),
'v' : ('test field', 'displacement', 'u'),
}
regions = {
'Omega' : 'all',
'Bottom' : ('vertices in (z < 0.1)', 'facet'),
'Top' : ('vertices in (z > 2.9)', 'facet'),
}
ebcs = {
'fixb' : ('Bottom', {'u.all' : 0.0}),
'fixt' : ('Top', {'u.[0,1]' : 0.0}),
}
integrals = {
'i' : 1,
'isurf' : 2,
}
equations = {
'linear' : """dw_lin_elastic.i.Omega(solid.D, v, u)
= dw_surface_ltr.isurf.Top(load.val, v)""",
'neo-Hookean' : """dw_tl_he_neohook.i.Omega(solid.mu_nh, v, u)
+ dw_tl_bulk_penalty.i.Omega(solid.K, v, u)
= dw_surface_ltr.isurf.Top(load.val, v)""",
'Mooney-Rivlin' : """dw_tl_he_neohook.i.Omega(solid.mu_mr, v, u)
+ dw_tl_he_mooney_rivlin.i.Omega(solid.kappa, v, u)
+ dw_tl_bulk_penalty.i.Omega(solid.K, v, u)
= dw_surface_ltr.isurf.Top(load.val, v)""",
}
solvers = {
'ls' : ('ls.scipy_direct', {}),
'newton' : ('nls.newton', {
'i_max' : 5,
'eps_a' : 1e-10,
'eps_r' : 1.0,
}),
'ts' : ('ts.simple', {
't0' : 0,
't1' : 1,
'dt' : None,
'n_step' : 101, # has precedence over dt!
'verbose' : 1,
}),
}
return locals()
##
# Pressure tractions.
def linear_tension(ts, coor, mode=None, **kwargs):
if mode == 'qp':
val = nm.tile(0.1 * ts.step, (coor.shape[0], 1, 1))
return {'val' : val}
def linear_compression(ts, coor, mode=None, **kwargs):
if mode == 'qp':
val = nm.tile(-0.1 * ts.step, (coor.shape[0], 1, 1))
return {'val' : val}
def store_top_u(displacements):
"""Function _store() will be called at the end of each loading step. Top
displacements will be stored into `displacements`."""
def _store(problem, ts, state):
top = problem.domain.regions['Top']
top_u = problem.get_variables()['u'].get_state_in_region(top)
displacements.append(nm.mean(top_u[:,-1]))
return _store
def solve_branch(problem, branch_function):
displacements = {}
for key, eq in six.iteritems(problem.conf.equations):
problem.set_equations({key : eq})
load = problem.get_materials()['load']
load.set_function(branch_function)
out = []
problem.solve(save_results=False, step_hook=store_top_u(out))
displacements[key] = nm.array(out, dtype=nm.float64)
return displacements
helps = {
'no_plot' : 'do not show plot window',
}
def main():
from sfepy.base.base import output
from sfepy.base.conf import ProblemConf, get_standard_keywords
from sfepy.discrete import Problem
from sfepy.base.plotutils import plt
parser = ArgumentParser(description=__doc__,
formatter_class=RawDescriptionHelpFormatter)
parser.add_argument('--version', action='version', version='%(prog)s')
parser.add_argument('-n', '--no-plot',
action="store_true", dest='no_plot',
default=False, help=helps['no_plot'])
options = parser.parse_args()
required, other = get_standard_keywords()
# Use this file as the input file.
conf = ProblemConf.from_file(__file__, required, other)
# Create problem instance, but do not set equations.
problem = Problem.from_conf(conf, init_equations=False)
# Solve the problem. Output is ignored, results stored by using the
# step_hook.
u_t = solve_branch(problem, linear_tension)
u_c = solve_branch(problem, linear_compression)
# Get pressure load by calling linear_*() for each time step.
ts = problem.get_timestepper()
load_t = nm.array([linear_tension(ts, nm.array([[0.0]]), 'qp')['val']
for aux in ts.iter_from(0)],
dtype=nm.float64).squeeze()
load_c = nm.array([linear_compression(ts, nm.array([[0.0]]), 'qp')['val']
for aux in ts.iter_from(0)],
dtype=nm.float64).squeeze()
# Join the branches.
displacements = {}
for key in u_t.keys():
displacements[key] = nm.r_[u_c[key][::-1], u_t[key]]
load = nm.r_[load_c[::-1], load_t]
if plt is None:
output('matplotlib cannot be imported, printing raw data!')
output(displacements)
output(load)
else:
legend = []
for key, val in six.iteritems(displacements):
plt.plot(load, val)
legend.append(key)
plt.legend(legend, loc = 2)
plt.xlabel('tension [kPa]')
plt.ylabel('displacement [mm]')
plt.grid(True)
plt.gcf().savefig('pressure_displacement.png')
if not options.no_plot:
plt.show()
if __name__ == '__main__':
main()